1.2.3.1. Моногибридное скрещивание.

Цель: Ознакомление с основными закономерностями наследования при моногибридном скрещивании.

Материал: В двух пробирках две альтернативные чистые линии мух дрозофил (P₁ и Р₂).

Оборудование: на каждого студента – морилка, часовое стекло,  кисточка, игла препаровальная, лупа; на группу – эфир, карандаши для письма по стеклу, вата.

Ход работы.

Анализ исходных линий. Убедиться, что мухи материнской и отцовской линий различаются по одной паре альтернативных признаков, при том, что детерминирующий ген локализован в одной из аутосом. Например, мухи альтернативных линий отличаются по окраске тела: мухи материнской линии имеют серое тело, а отцовской – темное.

Обозначить признаки и аллели гена, применяя стандартную символику (см. табл. 1), например:

e⁺– серое тело

e – тёмное тело

Написать две схемы скрещиваний при получении F₁ и F₂. Составить решетку Пеннета для F₂.

Анализ гибридов первого поколения. Убедиться, что все мухи имеют одинаковый фенотип, т.е. установить факт доминирования одного признака над другим и единообразия гибридов первого поколения (I закон Менделя).

Анализ гибридов второго поколения. Убедиться, что среди мух есть особи как с рецессивным, так и с доминантным признаками, т. е. установить явление расщепления (II закон Менделя). Подсчитать отдельно количество мух с альтернативными признаками.

Для проведения статистической обработки данных необходимо заполнить таблицу 2 (n – количество особей).

Таблица 2. Распределение особей F₂ по фенотипическим классам.

Далее проводится статистическая обработка полученных результатов. Наиболее адекватный для этого случая критерий Пирсона или критерий согласия  (читается «хи-квадрат») [2]. Этим методом можно определять степень расхождения между эмпирическими и теоретически ожидаемыми частотами, а также степень расхождения между двумя эмпирическими распределениями (второй случай рассматривается ниже в разделе 2.4.). Чем больше расхождение между двумя сопоставляемыми распределениями, тем больше эмпирическое значение .

Для нахождения  обычно используется следующая формула:

где О – фактически наблюдаемое, а Е – теоретически ожидаемое число или показатель для данной группы.

Ограничения критерия следующие.

1. Объем выборки должен быть достаточно большим: n>30. Точность критерия повышается при больших п.

2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5 особей.

3. Группировка на классы должна быть одинаковой во всех сопоставляемых распределениях.

4. Классы должны быть неперекрещивающимися: если наблюдение отнесено к одному классу, то оно уже не может быть отнесено ни к какому другому классу. И, очевидно, что сумма наблюдений по классам всегда должна быть равна общему количеству наблюдений.

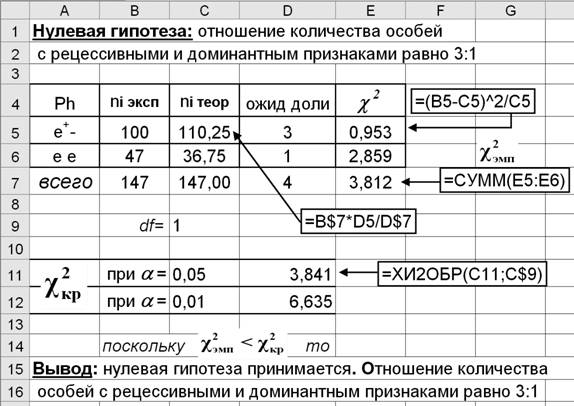
Анализ гибридов второго поколения методом

Доказать, что количество мух – особей с рецессивным и с доминантным признаками, равно отношению 3 : 1.

Расчеты производятся в среде MS Excel по следующей схеме (рис. 3).

Рис. 3. Скриншот расчетного листа MS Excel

1. Заносятся необходимые текстовые данные – пояснения и комментарии.

2. Заносятся исходные данные – эмпирические частоты (B5:B6), уровни значимости* (D11:D12), величины ожидаемых долей (D5:D6), а также в ячейку C9 вводится число степеней свободы df = 1 (количество классов минус единица умножить на количество признаков минус единица). Для общности можно использовать формулу =СЧЁТ(B5:B6)-1, которой определяется число степеней свободы df при сравнении двух рядов частот.

3. В ячейку B7 заносится формула подсчета общего числа наблюдений =СУММ(B5:B6). От ячейки B7 горизонтальным автозаполнением определяются C7:E7.

4. В ячейку С5 заносится формула, определяющая теоретическое значение частоты =B$7*D5/D$7. Механизмом вертикального автозаполнения по C5 вводится значение C6.

5. В ячейку D5 заносится формула, определяющая значение критерия  =(B5-C5)^2/C5. Механизмом автозаполнения по D5 вводится значение D6.

6. В ячейке D11 определяется значение  для первого (C11) доверительного уровня a=0,05 формулой =ХИ2ОБР(C11;С$9). Выполняется автозаполнение для ячейки D12.

7. Сравниваются  со значениями  (см. рис. 3). Поскольку , то формулируется вывод: нулевая гипотеза принимается на обоих уровнях значимости. Отношение количества особей рассмотренных фенотипических классов равно 3 : 1.