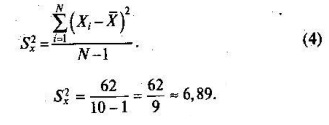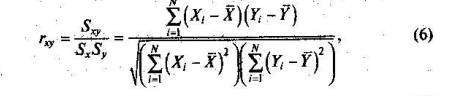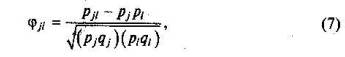Лекция 12. Классическая теория и методики конструирования тестов.

 

1.      Основные этапы конструирования теста.

2.      Традиционная теория тестов.

3.      Математико-статистический анализ тестов и тестовых заданий.

4.      Показатели связи между заданиями теста.

5.      Оценка характеристик заданий теста.

 

1. Основные этапы конструирования теста

Перечень этапов и их очередность. Процесс создания теста, его научного обоснования, переработки и улучшения можно разбить на ряд этапов, представленных ниже.

1. Определение цели тестирования, выбор вида теста и подхода к его созданию.

2. Концептуальный выбор конструкта (переменной измерения).

3.  Анализ содержания учебной дисциплины и планирование содержания теста, априорный выбор длины теста и времени его выполнения, разработка спецификации теста.

4. Определение структуры теста, форм заданий и стратегии их расположения в тесте.

5. Создание предтестовых заданий.

6. Отбор заданий в тест и их ранжирование согласно выбранной стратегии предъявления на основании априорных авторских оце­нок трудности заданий.

7. Экспертиза формы предтестовых заданий и содержания-теста.

8. Коррекция заданий и теста по результатам экспертизы.

9.  Разработка методики апробационного тестирования, инст­рукций для учеников и преподавателей, проводящих апробацию

теста.

10. Формирование репрезентативной выборки апробации.

11. Проведение апробационного тестирования.

12. Проверка результатов выполнения теста (автоматизирован­ная или ручная), подготовка эмпирических данных тестирования к виду, удобному для обработки и проведения анализа.

13. Статистическая обработка результатов выполнения теста (ав­томатизированная с помощью специального программного обес­печения).

14. Анализ и интерпретация результатов обработки в целях улуч­шения качества теста. Проверка соответствия характеристик теста научно обоснованным критериям качества.

15. Коррекция содержания и формы заданий на основании дан­ных предыдущего этапа. Чистка теста и добавление новых заданий для оптимизации диапазона значений параметра трудности и улучшения системообразующих свойств заданий теста. Оптимизация длины теста и времени его выполнения на основании статисти­ческих оценок характеристик теста Оптимизация порядка распо­ложения заданий в тесте.

16.  Повторение этапа апробации для выполнения очередных шагов по повышению качества теста.

17. Интерпретация данных обработки, установление норм тес­та и создание шкалы для оценки результатов испытуемых.

Апробация, анализ и коррекция теста. Апробация теста неодно­кратно повторяется. Обычно на разработку стандартизованного те­ста уходит не менее 3—4 лет, поскольку для апробации важно не только сформировать репрезентативную выборку учащихся, но и выбрать подходящее время в учебном процессе.

При разработке теста возникает своеобразный цикл, так как после его чистки создателю приходится возвращаться, к этапу ап­робация и анализа эмпирических данных тестирования, причем, как правило, не один раз,

Тщательная коррекция теста необходима особенно в тех случа­ях, когда тест должен быть стандартизован, а его результаты пла­нируется использовать для принятия административно-управлен­ческих решений в образовании.

2. Классическая (традиционная) теория тестов

Основное предположение классической теории тестов. Предпо­ложение о существовании истинного балла (true score) является основополагающим в классической теории тестов.

Нередко в одномерных измерениях истинный балл называют параметром учащегося, при этом предполагается, что каждому ученику можно поставить в соответствие единственное на момент измерения значение параметра, не зависящее от применяемого теста. В целом истинный балл — это идеализированная константа испытуемого в гипотетической генеральной совокупности зада­ний бесконечного теста.

Постулаты классической теории тестов. Помимо предположе­ния о существовании истинного балла в классической теории те­стов выделяют несколько постулатов, позволяющих построить ма-тематико-статистический аппарат для разработки научно обосно­ванных тестов и оценки качества результатов педагогических из­мерений [60; 81]. Эти постулаты связаны с предположениями:

- о равенстве ковариаций результатов тестирования по парал­лельным формам;

- о приближении средних значений ошибок измерения истин­ных баллов к нулю при числе тестирований, стремящемся к бес­конечности;

 - о инвариантности истинных баллов относительно различных параллельных форм теста;

- о континуальном (непрерывном) распределении истинных баллов в генеральной совокупности учащихся;

 - о нормальном законе распределения наблюдаемых баллов, истинных баллов и ошибок измерения.

 

3. Математико-статистический анализ качества тестов и тестовых заданий на основе

классической теории тестов

 

Матрица тестовых результатов. Если за каждый правильный ответ на задание испытуемому давать один балл, а за неправиль­ный ответ или пропуск задания — нуль баллов, то профиль отве­тов учащегося будет иметь вид последовательности из единиц и нулей. Поскольку каждая единица или нуль появляются в резуль­тате взаимодействия испытуемого с заданием, то наиболее адек­ватной формой представления наблюдаемых результатов выпол­нения теста будет служить матрица, т.е. прямоугольная таблица, сводящая воедино профили ответов учащихся (строки из оценок учащегося по всем заданиям теста) и профили заданий теста (столб­цы из оценок всех учащихся по каждому заданию теста).

Интегрирование данных тестирования в форме матрицы удоб­но для обработки и отражает взаимодействие множеств испытуе­мых и заданий, происходящее при выполнении теста (рис. 21).

При геометрической интерпретации этого взаимодействия по горизонтальной оси откладываются оценки параметра трудно­сти заданий теста, по вертикальной — оценки подготовленно­сти тестируемых учащихся. Взаимодействие между i-м испытуе­мым и j-м заданием порождает наблюдаемый ответ Х_ij, который при дихотомической оценке принимает одно из двух значений (см. табл. 6).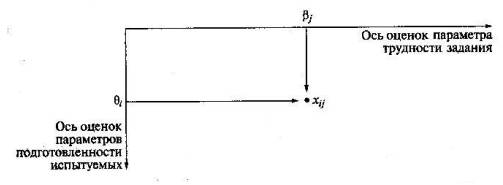

Рис.21 Геометрическая интерпретация взаимодействия множеств испытуемых и заданий теста

 

Таблица 6

 

 

Правило дихотомического оценивания ответа

 

 

Таблица 7

Матрица наблюдаемых результатов выполнения теста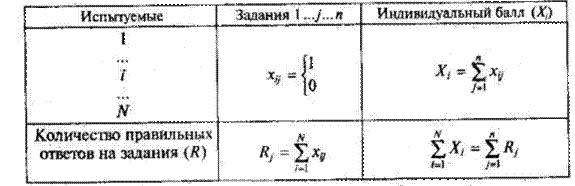

Общий вид матрицы наблюдаемых результатов выполнения N учащимися n заданий теста при дихотомических оценках по зада­ниям приведен в табл. 7.

Справа в матрице, в вертикальном столбце, содержатся инди­видуальные баллы учеников X_i (i=1,2,..., N), которые получают­ся суммированием единиц по горизонтали в каждом профиле от­ветов, учащегося. Сложение единиц в столбцах по профилям ответов на п заданий теста позволяет получить числа Ri (j=1, 2,..., n), соответствующие количеству правильных ответов на задания теста.

 

Таблица 8

Матрица результатов тестировании

После занесения результатов выполнения теста в матрицу на­чинается этап математико-статистической обработки, который включает ряд шагов. Из дидактических соображений для иллюст­рации методов обработки выбрана небольшая матрица, когда 10 учеников отвечали всего на 10 заданий теста (табл. 8). Однако все формулы и подсчеты, обсуждаемые в разделе, могут быть распро­странены на любые выборки испытуемых и применимы к тестам любой длины.

Первый шаг математико-статастической обработки эмпиричес­ких данных тестирования. На первом шаге обработки данных тес­тирования подсчитываются индивидуальные баллы и число пра­вильных ответов на каждое задание теста. Для подсчета индивиду­ального балла суммируются все единицы, полученные учащимся за правильно выполненные задания теста. Например; четвертый испытуемый выполнил правильно 9 заданий, поэтому его инди­видуальный балл равен 9. Для удобства полученные индивидуаль­ные баллы Xi{i =1,2, ... ,10) приводятся в последнем столбце матрицы результатов (табл. 9).

Число правильных ответов на каждое задание R_i , также получа­ется суммированием единиц, но уже расположенных по столбцам, и размещается в матрице результатов в последней строке под номером соответствующего задания теста.

 

Таблица 9

Матрица результатов с индивидуальными баллами испытуемых и количеством правильных ответов на задания теста

Номер испы туемого i	Номер заданий j										Индивиду альные баллы (множество Xi)
11	22	33	44	55	66	77	88	99	110
1	11	11	11	11	11	11	10	00	00	00	6
2	11	.1	00	00	00	00	00	00	00	00	2
3	00	00	00	00	00	00	00	11	00	00	1
4	1I	11	00	11	11	11	11	11	11	11	9
5	01	00	11	00	11	11	00	00	00	00	4
6	11	11	11	10	00	00	00	11	00	10	4
7	11	.1	11	11	10	11	00	00	00	00	5
8	11	11	11	11	00	00	00	00	00	00	4
9	11	11	11	11	11	11	11	11	11	00	9
10	11	.1	11	11	11	00	01	00	00	00	6
Число прави льных ответов (мно­жество Rj)	99	88	77	66	55	55	33	44	22	11	50

Второй шаг математико-статистической обработки эмпириче­ских данных тестирования. На втором шаге обработки данных осу­ществляется упорядочение матрицы результатов тестирования. Для этого производится перестановка столбцов, числа R_i, располага­ются в порядке убывания. Затем меняются местами строки матри­цы так, чтобы верхняя строка соответствовала обучаемому с ми­нимальным индивидуальным баллом. Значения X, располагаются сверху вниз в порядке возрастания. Упорядоченная матрица дан­ных тестирования приведена в табл. 10.

Третий шаг математико-статистической обработки эмпириче­ских данных тестирования. На данном этапе производится графи­ческая интерпретация распределений эмпирических данных, ко­торые можно представить в виде полигона, гистограммы или сгла­женной кривой (процентилей, огивы). Для графической интер­претации результатов учащихся необходимо их предварительное упорядочение в виде несгруппированного ряда произвольной фор­мы (табл. 11), ранжированного ряда (табл. 12), частотного распре­деления или распределения сгруппированных частот [1; 18; 59].

В табл. 11 содержатся индивидуальные баллы испытуемых, взя­тые из последнего столбца матрицы эмпирических результатов выполнения теста (см. табл. 9). В табл. 12 эти баллы располагаются в порядке возрастания слева — направо, а также приводятся места (ранги) испытуемых, соответствующие их индивидуальным бал­лам.

 

Таблица 10

Упорядоченная матрица данных тестирования

 

Таблица  11

Несгруппированный ряд

 

Таблица 12

Ранжированный ряд

 

 

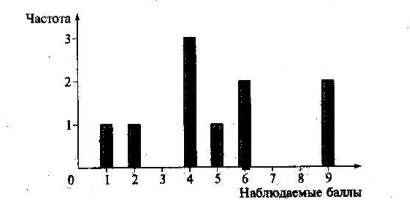
Данные таблицы удобны для подведения итогов тестирования в работе педагога, поскольку в классе распределения сырых бал­лов вполне достаточно для сообщения тестовых результатов уче­никам. Например, балл 6 обеспечивает первому испытуемому ранг 5 в группе из 10 учеников. Аналогичным образом можно интер­претировать любую оценку ученика в терминах рангов. Очевидно, что равным баллам приписываются равные ранги.

Если группа учащихся велика, то для определения рангов ис­пользуют классификацию оценок по распределению частот или строят сгруппированное частотное распределение. По ряду час­тотного распределения можно получить графическое представле­ние результатов тестирования в виде полигона частот и гисто­граммы — последовательности столбцов, каждый из которых опирается на единичный (разрядный) интервал и высота которых пропорциональна частоте наблюдаемых баллов [18; 59].

 

Рис. 22. Столбиковая гистограмма для распределения баллов в матрице, представленной в табл. 9

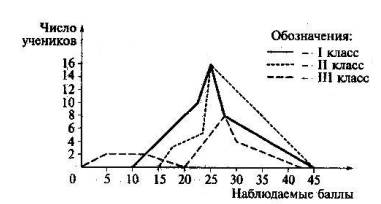
Рис. 23. Сравнение результатов тестирования

 

Например, матрице, представленной в табл. 10, соответствует гистограмма, приведенная на рис. 22. Середина столбца совмеща­ется с серединой интервала разряда, длина которого равна одно­му баллу.

Для сравнения двух или более распределений обычно исполь­зуют полигоны частот, так как при наложении гистограмм полу­чается довольно запутанная картина.

Например, с помощью полигонов можно сравнить результаты выполнения теста учащимися различных классов, имеющих оди­наковое количество учеников (рис. 23). На рисунке отчетливо вид­но значительное сходство в результатах тестирования у первых двух классов, имеющих довольно похожие полигоны распределе­ния оценок.

Четвертый шаг математико-статистической обработки эмпири­ческих данных тестирования. На данном этапе обработки данных оцениваются меры центральной тенденции в распределении ре­зультатов тестирования, предназначенные для выявления той точ­ки, вокруг которой в основном группируются все результаты вы­полнения теста [1; 18; 59]. При анализе результатов тестирования можно использовать разные способы определения такой централь­ной точки. Наиболее простой из них основан на выявлении моды распределения.

Мода — это такое значение, которое встречается наиболее часто среди результатов выполнения теста. Например, для дан­ных матрицы, представленной в табл. 10, модой является балл «4», потому что он встречается чаще (три раза) любого другого значения балла. Распределение может иметь одну или несколь­ко мод. В случае существования двух мод распределение называ­ется бимодальным. Если все значения баллов учеников встреча­ются одинаково часто, принято считать, что моды у распределе­ния нет.

Среднее выборочное (среднее арифметическое) определяется сумми­рованием всех значений совокупности баллов и последующим делением на их число. Для индивидуальных баллов Х_1, Х₂.....X_N группы N испытуемых среднее значение X будет  

 

 

 

 

 или          

   

Среднее арифметическое индивидуальных баллов испытуемых для рассмотренного выше примера матрицы (см. табл. 10) равно

 

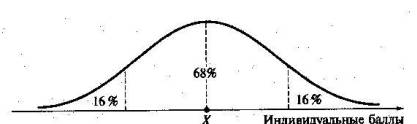
В отличие от моды, фиксирующей одно или несколько значе­ний, на величину среднего влияют значения всех результатов рас­пределения. Таким образом, среднее арифметическое характери­зует все распределение в целом. Оно обобщает индивидуальные особенности составляющих распределения на основе уравнива­ния отдельных значений рассматриваемой величины. С другими свойствами среднего выборочного можно познакомиться в учеб­нике по статистике.

Меры центральной тенденции полезны при оценке качества теста в том случае, когда есть результаты апробации теста на ре­презентативной выборке учеников. Обычно считают, что хороший нормативно-ориентированный тест обеспечивает нормальное рас­пределение индивидуальных баллов репрезентативной выборки учеников, когда среднее значение баллов находится в центре рас­пределения, а остальные значения концентрируются вокруг сред­него по нормальному закону, т.е. примерно 70 % значений в цен­тре, а остальные сходят на нет к краям распределения, как пока­зано на рис. 24.

 

Рис. 24. Нормальная кривая распределения индивидуальных баллов

 

Нормальная кривая — изобретение математиков - в сглажен­ном идеальном виде описывает реальный полигон частот. На прак­тике никогда не была и не будет получена совокупность данных, распределенных точно по нормальному закону, просто иногда полезно, допуская определенную ошибку, утверждать, что рас­пределение эмпирических данных близко к нормальной кривой. Нормальное распределение унимодально и симметрично, т.е. по­ловина результатов, расположенная ниже моды, в точности со­впадает с другой половиной, расположенной выше, а мода и сред­нее значение равны.

Если тест обеспечивает распределение баллов, близкое к нор­мальному, то это означает, что с его помощью можно определить устойчивое среднее, которое принимается в качестве одной из репрезентативных норм выполнения теста. Обратный вывод неве­рен: устойчивость тестовых норм вовсе не предполагает обязатель­ного нормального распределения эмпирических результатов вы­полнения теста. Таким образом, правильно сконструированный нормативно-ориентированный тест на репрезентативной выбор­ке учеников должен обеспечивать близкое к симметричному рас­пределение индивидуальных баллов, когда мода и среднее значе­ние примерно равны, а остальные результаты расположены во­круг среднего по нормальному закону.

Пятый шаг математико-статистической обработки эмпирических данных тестирования. На данном этапе определяются описатель­ные характеристики, служащие мерами изменчивости в распре­делении данных по гесту [1; 18; 59]. Введение мер изменчивости связано с необходимостью выявления дополнительных основа­ний для сравнения различных распределений по тестам. Если рас­пределения имеют одинаковые средние, то, оценивая и анализи­руя, меры изменчивости, можно выявить существенные отличия в качестве тестов.

Характеристика изменчивости указывает на особенности раз­броса эмпирических данных вокруг среднего значения: баллов. Отдельные значения индивидуальных баллов могут быть тесно сгруппированы вокруг своего среднего балла или, наоборот, сильно удалены от него. Для отражения характера рассеяния отдельных значений вокруг среднего используются различные меры: размах, дисперсия и стандартное отклонение.

Размах измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Напри­мер, для распределения индивидуальных баллов, представлен­ных в, табл. 10, размах равен 9-1 = 8. Вариационный размах легко вычисляется, но при характеристике распределения баллов по тесту используется крайне редко. Во-первых, размах является весьма приближенным показателем, так как не зависит от степени из­менчивости промежуточных значений, расположенных между крайними значениями в распределении баллов по тесту, Во-вторых, крайние значения индивидуальных баллов, как правило, ненадежны, поскольку содержат в себе значительную ошибку из­мерения. В этой связи более удачной мерой изменчивости считает­ся дисперсия.

Подсчет дисперсии основан на вычислении отклонений Х₁ - Х (i =1, 2, …, N) каждого значения показателя от среднего ариф­метического в распределении. Для ученика с индивидуальным бал­лом выше среднего значение разности Х₁-X будет положитель­но, а для тех, у кого, результат ниже X,  отклонение Х₁ - X будет меньше нуля.

Если просуммировать все отклонения, взятые со своим знаком, то для симметричных распределений сумма будет равна нулю. Чтобы отрицательные и положительные слагаемые не уничтожали друг друга, каждое отклонение возводят в квадрат, а затем находят сумму квадратов отклонений. Эта сумма будет большой, если результаты тестирования отличаются существенной неоднородностью, и малой — в случае близких результатов испытуемых по тесту. Для матрицы, представленной в табл. 9, сумма квадратов отклонений будет равна

Величина суммы зависит от размера выборки учеников, вы­полнявших тест, поэтому для сопоставимости мер изменчивости распределений, отличающихся по объему, каждую сумму делят на N - 1, где N - число учеников, выполнявших тест. Определя­емая таким образом мера изменчивости называется исправленной дисперсией. Она обычно обозначается символом S²_x и вычисляет­ся по формуле

Для рассматриваемого примера

 

Кроме дисперсии для характеристики меры изменчивости рас­пределения удобно использовать еще один показатель вариации, который называется стандартным отклонением и вычисляется путем извлечения квадратного корня из дисперсии:

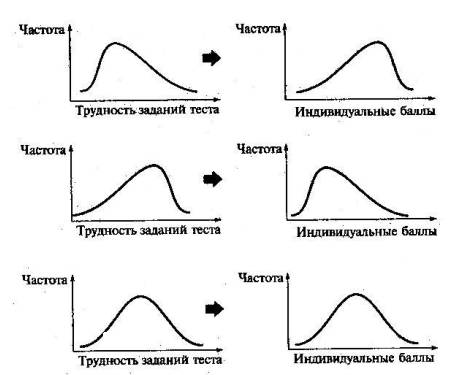
Для рассматриваемого примера данных тестирования 6,89=2,62. Свойства дисперсии и стандартного отклонения рассматриваются подробно в учебниках по статистике. Заинтере­сованному читателю можно порекомендовать, например, книгу Дж. Гласс и Дж. Стенли «Статистические методы в педагогике и психологии» [18].

Дисперсия играет важную роль в оценке качества тестов. Низ­кая дисперсия указывает на плохое качество нормативно-ориен­тированного теста, поскольку не обеспечивается высокий диффе­ренцирующий эффект. Излишне высокая дисперсия, характерная для случая, когда все учащиеся различаются по числу выполнен­ных заданий, также требует переработки теста из-за существен­ного отличия вида распределения баллов от плакируемой нор­мальной кривой.

Использование стандартного отклонения как меры вариации особенно эффективно для нормального распределения баллов испытуемых, поскольку в этом случае можно прогнозировать про­цент данных, лежащих внутри одного, двух и трех стандартных отклонений, откладываемых от центра распределения. В любом нормальном распределении приблизительно 68% площади под кривой лежит в пределах одного стандартного отклонения, откла­дываемого влево и вправо от среднего (т.е. X ± 1S_x); 95% площа­ди под кривой расположено в пределах двух. S_x, (X±2S_X); 99,7% площади под кривой — в пределах трех S_x,. (X ± 3S_х). Из всех нор­мальных кривых наиболее удобна единичная, площадь под кото­рой равна 1. Для нее среднее значение равно нулю (z=0), а стан­дартное отклонение единице (а_г = 1).

При использовании теста необходимо помнить о том, что по­лучаемое распределение индивидуальных баллов учащихся явля­ется следствием подбора трудности заданий теста, как показано на рис. 25.

.Для верхнего распределения слева характерно смещение в сто­рону легких заданий, поэтому большая часть учащихся выполнит почти все задания теста и получит высокие индивидуальные бал­лы, показанные на правом верхнем рисунке. Средние графики отражают тенденцию к приоритетному подбору самых трудных заданий при разработке теста и вытекающий отсюда всплеск у начала горизонтальной оси там, где располагаются низкие инди­видуальные баллы. Тест, представленный на нижнем графике сле­ва, обладает сбалансированной трудностью, что автоматически приводит к нормальности распределения индивидуальных баллов репрезентативной выборки учеников.

Это позволяет считать полученное распределение устойчивым по отношению к генеральной совокупности, а также помогает определить репрезентативные нормы выполнения теста.

Последующие шаги обработки данных предназначаются для оценивания мер симметрии и островершинности кривых распре­делений [1; 18; 60; 63] и выполняются обычно при разработке тестов административно-управленческого предназначения не «ру­ками», а с помощью специальных статистических пакетов для ПК.

Рис. 25. Связь распределения индивидуальных баллов и трудности зада­ний теста 

 

4. Показатели связи между заданиями теста

 

Корреляция результатов учащихся по заданиям. Для итогового контроля полезно вычислять показатели связи между результата­ми учеников по отдельным заданиям теста. При этом важно по­нять, существует ли тенденция, когда одни и те же ученики до­биваются успеха в какой-либо паре заданий теста, или состав уче­ников, добивающихся успеха, полностью меняется при переходе одного задания теста к другому.

Ответ на вопрос о существовании связи между двумя наборами данных получают с помощью корреляции [18; 60; 63]. Для ее оце­нивания в общем случае применяют коэффициент корреляции Пирсона г,у, значения которого меняются в интервале от -1 до +1.

где X_l, ..., X_N — первый набор данных со средним значением X, а Y₁,,.,., Y_N — второй набор данных со средним значением Y.

При исследовании связи между наборами данных необходимо правильно выбрать вид и форму показателя, зависящие от шкал, в которых представлены данные [18]. В частности, для оценки свя­зи между результатами выполнения учащимися двух заданий тес­та коэффициент корреляции Пирсона r_ху необходимо преобразо­вать, поскольку результаты выполнения заданий представляются в дихотомической шкале (столбцы из нулей и единиц в матрице данных по тесту). Преобразованный коэффициент Пирсона для дихотомических данных называется коэффициентом «фи» и вы­числяется по формуле

где Pji — доля испытуемых, выполнивших правильно оба задания с номерами j и l, т.е. доля тех, кто получил «1» по обоим задани­ям; p_j — доля испытуемых, правильно выполнивших одно j-е за­дание, q_j  =1 – р_j, P_l — доля испытуемых, правильно выполнивших l-е задание теста, q_t = 1 -р,.

Анализ значений коэффициента корреляции р позволяет выя­вить неудачные задания теста, которые отрицательно коррелиру­ют с большинством остальных заданий и, следовательно, изме­ряют нечто иное, чем та переменная, для которой предназначал­ся тест. Отрицательные значения коэффициента корреляции ука­зывают на определенный просчет разработчиков в содержании заданий, которые рекомендуется удалить из теста. Наиболее распространенная причина появления отрицательной корреляции — отсутствие предметной чистоты содержания — встречается при разработке самых разных тестов довольно часто. Предметная чистота — скорее идеализируемое, чем реаль­ное, требование к содержанию любого теста. Так, в любом тесте по физике встречаются задания с большим количеством мате­матических преобразований, в тесте по биологии — задания, требующие, серьезных знаний по химии, в тесте по истории — за­дания, рассчитанные на выявление культурологических знаний, и т.п. Поэтому можно лишь стремиться к тому, чтобы при выпол­нении каждого задания доминировали знания по проверяемому предмету.

Для тематических тестов характерна высокая корреляция меж­ду заданиями, так как они в большинстве случаев имеют слабо варьирующее исходное содержание, что вполне объясняется на­значением теста. Однако в итоговых тестах по возможности стара­ются избегать высокой корреляции между заданиями, поскольку вряд ли имеет смысл включать в итоговый тест несколько зада­ний, оценивающих одинаковые содержательные элементы. В ито­говых тестах обычно стремятся к невысокой положительной кор­реляции, когда значения коэффициента варьируют в интервале (0; 0,3) и каждое задание вносит свой вклад в общее содержание теста.

Бисериальный коэффициент корреляции. Бисериальный коэф­фициент корреляции используется в том случае, когда один на­бор значений распределения задается в дихотомической шкале, а другой — в интервальной. Под эту ситуацию подпадает подсчет корреляции между результатами выполнения каждого задания (ди­хотомическая шкала) и суммой баллов испытуемых по заданиям теста (интервальная или квазиинтервальная шкала). С помощью подсчета значений бисериального коэффициента корреляции оце­нивается валидность, иногда называемая показателем дифферен­цирующей способности (дискриминативности) заданий теста.

Объяснение, на котором основан вывод формулы для подсчета бисериального коэффициента корреляции, приводится в ряде исследований [18; 60; 73]. Его вычисление требует использования специальных таблиц для нахождения ординат стандартной нор­мальной кривой и определенной математической подготовки. По­этому нередко используют другой коэффициент корреляции, на­зываемый точечным бисериальным коэффициентом — r_pbis. Осно­ванием для подобной замены служит близость значений этих ко­эффициентов: первый незначительно превышает второй, если они подсчитаны для одних и тех же наборов данных из распределений. Однако формула для r_pbis намного проще, поэтому именно ему часто отдают предпочтение в практической работе.

Анализ значений коэффициента бисериальной корреляции, подсчитанного для оценки связи результатов по каждому заданию с суммой баллов по тесту, позволяет выявить задания с низкой валидностью, с помощью которых трудно отделить хорошо под­готовленных учащихся от слабо подготовленных учащихся тести­руемой группы. Значения, близкие к нулю, указывают на низкую дифференцирующую способность заданий теста. Если коэффици­ент бисериальной корреляции принимает отрицательные значе­ния, задание следует удалить из теста, так как при выполнении такого теста слабые ученики выполняют его верно, а сильные выбирают неверный ответ либо пропускают задание.

5. Оценка характеристик заданий теста

 

Оценка трудности заданий по классической теории тестов. Оценка трудности тестовых заданий в классической теорий тестов осуще­ствляется по формуле

 где pj — доля правильных ответов на j-е задание; R_j -  количество учеников, выполнивших  j-е задание верно; N- число учеников в тестируемой группе; j — номер задания теста (j= 1, 2 , …, n). Трудность задания нередко выражают в процентах. Для этого оцен­ку, полученную по формуле (8), умножают на 100%.

Долю правильных ответов на задание p _j правильнее было бы назвать легкостью задания, в то время как трудность ассоциирует­ся с долей неправильных ответов q_j, которая находится путем вы­читания p_j из единицы: q_j = 1 - p_j. Однако по сложившейся тради­ции в классической теории тестов за трудность задания принима­ется именно доля pj.

Подбор заданий по трудности в нормативно-ориентированных тестах. В хорошо сбалансированном по трудности тесте всегда есть несколько самых легких заданий со значениями р -> 0 и несколь­ко самых трудных со значением р -> 1. Остальные задания по зна­чениям р занимают промежуточное положение между этими край­ними ситуациями и имеют в основном трудность 60—70 %.

Дополнительный аргумент в пользу преимущественного вклю­чения заданий средней трудности с р = 0,5 связан с подсчетом дис­персии по каждому заданию теста, которая для дихотомического набора данных будет равна оj, = p_jq_j (j =1,2, ..., п). Так как произ­ведение p_jq_j; достигает максимального значения (0,5 • 0,5 = 0,25) при pj= 0,5 - qj, в рамках нормативно-ориентированного подхода наи­более удачными считаются задания средней трудности р = q = 0,5, обеспечивающие максимальный вклад в общую дисперсию теста. В пользу преимущественного выбора заданий средней трудно­сти также говорит подсчет ошибки измерения, которая уменьша­ется по мере продвижения к центру, где расположены задания средней трудности, и увеличивается на концах распределения

Связь оценок трудности и валидностн заданий. Интересна взаи­мосвязь показателей трудности и валидности (дискриминативности) заданий теста. Задания с высокой дискриминативностъю обыч­но имеют среднюю трудность, поскольку именно для них харак­терен в первую очередь высокий дифференцирующий эффект. Однако обратное заключение неверно. Задания с р = 0,5 могут иметь как высокий, так и низкий дифференцирующий эффект.

При подсчете статистик по тесту всегда проводится проверка значимости полученных оценок дисперсии, асимметрии и т д. Для этого к данным, собранным по тесту, необходимо добавить информацию о принимаемом уровне риска допущения ошибки в статистическом выводе. Наиболее приемлемым для педагогичес­ких измерений является уровень в 5 %, который допускает ошиб­ку в 5 случаях из 100. После выбора степени риска проверка значимости проводится одним из описанных в литературе методов [18; 74].

Гомогенность (содержательная однородность) задания. При кон­струировании теста необходимо иметь четкое представление о со­держании заданий, которые предполагается включить в оконча­тельную версию теста. При одномерных измерениях содержание заданий должно отвечать свойству гомогенности, указывающему на степень его однородности с точки зрения оцениваемого пара­метра подготовленности ученика. Таким образом, гомогенность (однородность) — это характеристика задания, отражающая сте­пень соответствия его содержания измеряемому свойству ученика. Степень гомогенности содержания обычно оценивают с помощью факторного и корреляционного анализа.

Группа с низкой подготовленностью			Группа с высокой подготовленностью
Испытуе­мый	Ответы на задание	Индивидуаль­ный балл по тесту	Испытуе­мый	Ответы на задание	Индивидуаль­ный балл по тесту
1	0	8	8	1	33
2	0	12	9	0	28
3	0	6	10	1	29
4	0	12	11	1	30
5	0	8	12	1	29
6	0	8	13	0	28
7	0	8	14	1	33

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8	0	11	8	1	32
9	1	13	9	1	32
10	0	4	10	1	33
11	1	14	11	0	34
12	1	13	12	1	35
13	1	10	13	1	34
14	1	9	14	1	38
15	0	8	15	1	37

 

Дайте интерпретацию полученных результатов. Наблюдается ли инва­риантность вычисленных характеристик задания относительно уровня подготовленности выборки? Как можно объяснить наличие (отсутствие) инвариантности?