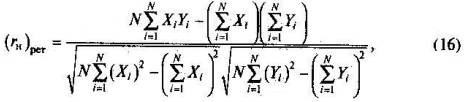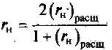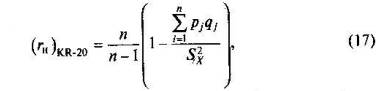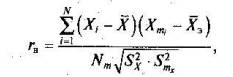Лекция 14. Оценивание надежности и валидности педагогических тестов.

 

1.      Реестовый метод.

2.      Метод параллельных форм.

3.      Метод расщепления теста.

4.      Метод Кьюдера- Ричардсона. Н

5.      адежность и стандартная ошибка измерения.

6.      Валидность гомогенных тестов.

 

 

1. Оценивание надежности ретестовым методом (двукратное тестирование)

 

Общие замечания о надежности и методах ее оценивания. Ввод­ные представления о надежности педагогических измерений были изложены в разделе 4.5, содержащем определение, концептуаль­ное обоснование и анализ надежности в контексте ее связи с дис­персией наблюдаемых баллов и ошибкой измерения. В том же раз­деле приведено определение коэффициента надежности теста — r_H, позволяющее сделать некоторые выводы о факторах, влияю­щих на ее величину.

Оценка надежности нормативно-ориентированных тестов про­водится различными методами, которые по способу осуществле­ния можно условно разделить на две группы [1; 60]. Первая группа методов базируется на двукратном тестировании, про­водимом с помощью одного и того же теста или с помощью двух параллельных форм теста. Вторая группа методов предпола­гает однократное тестирование при оценке надежности теста. На практике стараются использовать вторую группу методов, посколь­ку организация повторного тестирования и разработка параллель­ных форм всегда сопряжены с определенными трудностями и до­полнительными затратами со стороны создателей тестов. Обычно вне зависимости от метода оценка надежности строится на под­счете корреляции между двумя наборами данных. Логика рассуж­дений при этом довольно проста: чем выше корреляция, тем на­дежнее тест.                             

  Для маленькой выборки корреляцию можно оценить визу­ально (табл. 13). В рассматриваемом гипотетическом примере три теста А, В и С из 10 заданий дважды выполняла одна и та же выборка из 10 учеников.

Тест А обладает оптимальной надежностью, так как результа­ты 10 учеников остались прежними: баллы и места учеников не изменились после повторного выполнения теста. Подсчет корре­ляции результатов первого и второго тестирования даст коэффи­циент корреляции, равный единице. Тест В полностью ненадежен: тот, кто имел самые высокие баллы в первом тестировании, по­лучает самые низкие баллы во втором тестировании после повторного применения этого же теста. Полное отсутствие воспро­изводимости баллов испытуемых указывает на минимальную на­дежность теста, близкую к -1. Тест С обеспечивает в целом хаотич­ное изменение результатов, хотя баллы отдельных учеников (3-го и 9-го) будут воспроизведены при повторном выполнении теста. Скорее всего, надежность третьего теста близка к нулю.

                                                                       

Таблица 13

Результаты двукратного выполнения трех тестов

 

 

Естественно, что рассмотренные гипотетические ситуации не встречаются в практике. Обычно коэффициент надежности при­нимает положительные значения, но никогда не бывает равен единице. Это относится даже к существующим десятилетия тестам, получившим всеобщее признание.

Подсчет коэффициента надежности. Ретестовый метод оценки надежности (test-retest reliability) основан на подсчете корреля­ции индивидуальных баллов испытуемых, полученных в резуль­тате двукратного выполнения ими одного и того же теста. Обыч­но повторное тестирование проводится через 1 —2 недели, когда испытуемые еще не успели забыть учебный материал и незначи­тельно продвинулись в усвоении новых знаний. При таких усло­виях повторного предъявления теста низкая корреляция между результатами тестирования будет следствием не изменения со­стояния испытуемых, а применения ненадежного теста.

Для подсчета коэффициента надежности по методу повторно­го тестирования используется формула

где (г_н)_рет — коэффициент надежности теста по ретестовому мето­ду; Xi — индивидуальный балл i-го испытуемого в первом тести­ровании; Yi — индивидуальный балл i-го испытуемого во втором тестировании (i = 1, 2, ..., N).

Пример подсчета. Используя данные табл. 9 (первое тестирова­ние) и добавляя к ним гипотетические данные второго тестиро­вания, можно с помощью табл. 14 подсчитать коэффициент надежности ретестовым методом.

После подстановки чисел из нижней строчки таблицы в формулу (16) коэффициент надежности будет равен (r_н)_рен=

указывает на невысокую надежность теста.

Применение ретестового метода может привести к ошибочным оценкам надежности в тех случаях, когда, проводится слишком близ­кое по времени повторное применение теста. Учащиеся запомина­ют ответы к заданиям и при повторном тестировании значительно повышают свои результаты, что искажает оценку надежности теста.

 

Пример данных для оценки надежности

 

Таблица  14

 

Номер учени­ка i	Балл при пер­вом тестиро­вании Xi	Балл при вто­ром тестиро­вании Yi	XiYi	(Xi)2	(Yi)2
1	6	5	30	36	25
2	2	4	8	4	16
3	1	2	2	1	4
4	9	7	63	81	49
5	4	6	24	16	36
6	4	3	12	16	9
7	5	7	35	25	49
8	4	6	24	16	36
9	9	. 7	63	81	49
10	6	8	48	36	64
	∑ =50	∑Yi=55	∑XiYi=309	∑(Xi)2=312	∑(Yi)2=337

 

2. Метод параллельных форм

 

Метод параллельных форм (parallel-form reliability) малоэффек­тивен в тех случаях, когда при тестировании используется один вариант теста. В некоторых странах, например в США, благодаря соблюдению всех требований к проведению тестирования приме­нение единственного варианта не снижает необходимый уровень информационной безопасности и обеспечивает при этом высо­кую сопоставимость результатов выполнения теста. Если тест только один, то для оценки надежности методом параллельных форм приходится создавать параллельный вариант теста, затем с затра­тами сил, средств и времени на апробацию доказывать правомер­ность гипотезы о параллельности и только потом оценивать на­дежность исходного теста.

Если параллельные варианты теста разрабатываются изначаль­но, как в ЕГЭ, оценка надежности методом параллельных форм также требует значительных трудозатрат. Необходима тщательная ротация вариантов в группе испытуемых для обеспечения сход­ных выборок учащихся на параллельных вариантах теста. Даже при стратификации выборки испытуемых и ротации вариантов досто­верность оценок надежности снижается из-за того, что параллель­ные формы — это скорее теория, чем реальность, поскольку на практике, несмотря на все усилия авторов, как правило, обнару­живаются статистически значимые различия в характеристиках па­раллельных вариантов. Для оценки надежности методом парал­лельных форм используется формула (16). В ней X_i (i= 1, 2,..., N) — индивидуальные баллы испытуемых в первой форме, a Y_i (i=1, 2,...., N) — индивидуальные баллы во второй форме. Далее все вычисления с точностью повторяют подробно рассмотренный пример (см. табл. 9).

 

3. Метод расщепления теста

(однократное тестирование)

Описание метода. Метод оценивания надежности, основанный на расщеплении результатов по тесту на две части (split-half method), наиболее распространен из-за своего удобства. Он по­зволяет вычислить коэффициент надежности при однократном выполнении учениками теста. Для оценки надежности результаты тестирования делят на две части: в одну включают данные испы­туемых по четным, а в другую — по нечетным заданиям, считая при этом, что получены сходные по содержанию части теста. Прав­да, деление на две части не единственный способ, возможны и другие варианты, когда выделяют большее число частей, при оценке надежности теста.  

Таблица 15

Сводная таблица для оценка надежности (метод расщепления)

 

 

Подсчет, коэффициента надежности. Для оценивания надежности методом расщепления результаты учеников заносят в табл. 15.

Далее для таблицы данных используют формулу (16), в кото­рой роль результатов в первом тестировании выполняют данные по четным, а во втором — по нечетным заданиям. Использование метода расщепления дает заниженные оценки надежности в силу того, что она оценивается для укороченного в 2 раза теста.

Коррекция коэффициента надежности. Для коррекции оценки надежности в соответствии с длиной исходного теста используется формула Спирмена—Брауна

 

где в числителе и знаменателе дроби стоит коэффициент надежности для половины заданий теста, а слева — скорректированный коэффициент на­дежности с учетом всех заданий теста.

Приведенный метод оценивания надежности имеет свои огра­ничения в применении. Он основан на допущении параллельно­сти двух половин теста, что не всегда и не в полной мере может оказаться верным. Корреляция двух половин возрастает по мере роста гомогенности теста. В этой связи метод, расщепления неред­ко называют методом оценки внутренней состоятельности {согла­сованности) теста (Internal-Consistency Method).

 

4. Метод Кьюдера—Ричардсона (для дихотомических оценок

по заданиям теста)

Описание метода. Метод Кьюдера—Ричардсона для оценки надежности, так же как и метод расщепления теста, основан на однократном тестировании, но в отличие от него не зависит от искусственных допущений о полной параллельности двух частей теста. Однако сфера его применения ограниченна, так как он го­дится лишь при использовании дихотомических опенок по ре­зультатам выполнения заданий гомогенных тестов.

Формула Кьюдера—Ричардсона. Формула Кыодера— Ричардсона (KR-20) имеет следующий вид:

p_j — доля правильных ответов на j-е задание; q_j — доля непра­вильных ответов, q_j = 1 – р_j; S_x² — дисперсия по распределению наблюдаемых баллов; п — число заданий теста [87].

Для матрицы данных, представленных в табл. 9, подсчитанная ранее исправленная дисперсия равна Sx2=6,89, а доли правильных ответов получаются делением чисел _Rj  в последней строке матрицы на 10. Сумма произведений долей правильных и неправильных отве­тов в таком случае будет равна 0,9*0,1+0,8*0,2 + 0,7 *0,3 + 0,6*0,4 + + 0,5*0,5 + 0,5 *0,5 + 0,3*0,7 + 0,4*0,6 + 0,2*0,8 + 0,1*0,9 = 1,9,

 

.

а коэффициент надежности

 

Общие рекомендации по применению метода Кьюдера—Ричард­сона. В целом при оценке надежности нельзя полагаться лишь на один показатель, поскольку каждый из них имеет свои ограниче­ния, смещающие оценки надежности теста в сторону завышения или занижения. Для достоверной проверки качества теста следует учитывать несколько показателей надежности, подсчитанных по разным формулам. В данном пособии приведена лишь небольшая их часть.

В качестве нижнего предела допустимых значений надежности обычно выбирают 0,7. При более низком значении использование теста вряд ли целесообразно в силу большой погрешности изме­рения. Бели тест разрабатывается профессионалами, то к нему предъявляют более жесткие требования. Как правило, тесты с на­дежностью менее 0,8 считаются непригодными в профессиональ­но организованных службах и центрах тестирования. Значения коэффициента надежности, превышающие 0,9, свидетельствуют о высоком качестве теста. Они желательны, но встречаются редко. Обычно в тестологической практике надежность тестов колеблет­ся в интервале (0,8; 0,9).

 

5. Надежность и стандартная ошибки измерения

 

Связь между стандартной ошибкой измерения и надежностью теста. Один из аспектов применения коэффициента надежности связан с определением стандартной ошибки измерения. Для уста­новления связи между стандартной ошибкой измерения и надеж­ностью теста необходимо преобразовать формулу (1) для коэф­фициента надежности теста, выделив в левой части S_Е². После пре­образования формулы относительно  S_Е² получится выражение

где S_x — стандартное отклонение по распределению индивиду­альных баллов; r_H — коэффициент надежности теста; S_E — стан­дартная ошибка измерения. Это выражение обычно используется для вычисления S_E по известным величинам r_н и S_x.

Для лучшего уяснения смысла показателя S_E можно представ вить, гипотетическую ситуацию, когда i-й испытуемый выполнял много раз один и тот же тест. Если предположить, что эффект запоминания отсутствует, то результаты тестирования образуют нормальное распределение вокруг истинного балла Т_i, со стандар­тным отклонением S_E. На практике S_E рассматривается как стати­стическая величина, отражающая степень точности отдельных измерений, поэтому величину S_E используют для определения границ доверительного интервала, внутри которого должен нахо­диться истинный балл оцениваемого ученика группы.

Построение доверительного интервала. Общераспространен под­ход, когда доверительный интервал выстраивается вокруг наблю­даемого показателя ученика как две симметричные окрестности (левая и правая), хотя это не совсем верно, поскольку речь долж­на идти об окрестностях, расположенных слева и справа от ис­тинного балла. Тем не менее этот факт вынужденно игнорируется в прикладных исследованиях в силу отсутствия истинного балла, и доверительный интервал при заданном риске допустить ошибку  t= 0,05 (в пяти случаях из ста) принимается равным (X_i - 1,96S_E, X_i + l,96S_E), где Xi — наблюдаемый балл i-го испытуемого; 1,96 — константа, табличное число, используемое при t =0,05.

Численный пример. Для рассматриваемого ранее примера мат­рицы тестовых результатов (см. табл. 9), коэффициента надежно­сти r_н= 0,78 и стандартного отклонения S_x= 2,62, вычисленного ранее для матрицы, S_E будет равно S_E =2,62√1-0,78 ≈1,23. В данном случае доверительный интервал для истинного балла первого ученика со значением Х₁.= 6 будет составлять (6 - 1,23; 6 +1,23) или (4,77; 7,23). Истинный балл первого ученика может находить­ся в любой точке этого интервала.

   Очевидно, что с ростом S_E границы доверительного интервала будут раздвигаться, и вместе с тем будут увеличиваться возмож­ные пределы отклонения истинного балла от наблюдаемых ре­зультатов измерения (величина отклонения наблюдаемых баллов от истинной компоненты измерения).

Предсказание истинных баллов на основе регрессионной модели. Методы регрессионного анализа позволяют прогнозировать оцен­ки истинных баллов испытуемых по распределению наблюдаемых баллов и коэффициенту надежности теста. Прогноз получается путем подстановки в регрессионное уравнение

 

T_i=X + r_н(X_i-X),

 

где Т_i — истинный балл; Xi — индивидуальный балл i-го испыту­емого; .X — среднее значение баллов испытуемых [60].

 

6. Валидность гомогенных тестов

 

Общие замечания. Валидность педагогических измерений рас­сматривалась ранее в разделе 4.5. Как правило, постановка целей создания теста носит комплексный характер, поэтому часто ва­лидность стараются проверить с разных позиций сообразно раз­личным направлениям использования теста. Например, норматив­но-ориентированный тест для приема абитуриентов в вузы дол­жен служить цели дифференциации испытуемых и прогностичес­ким целям, так как необходимо не только выделить лучших аби­туриентов в момент приема, но и спрогнозировать успешность дальнейшего обучения зачисленных в вузы абитуриентов.

Критерии для оценки валидности. Как было отмечено ранее, оце­нивание валидности всегда проводится путем соотнесения харак­теристик результатов измерения с внешними критериями [1; 69; 86]. В качестве таких критериев могут выступать оценки экспертов при анализе содержания теста и его адекватности целям измере­ния (содержательная валидность), результатов по другим тестам (конструктная валидность), успешности дальнейшего обучения (прогностическая валидность).

Высокая корреляция между анализируемыми результатами ис­пытуемых и внешними критериями подтверждает высокую валид­ность теста. Основная трудность при такой ваяидизации носит не практический» а методологический характер, поскольку она со­стоит в выборе значимого внешнего критерия.

Связь надежности и валидности. Для повышения полноты охва­та содержания и роста содержательной валидности теста жела-тельно отбирать задания с малыми коэффициентами интеркорре­ляции. К противоположному выводу легко прийти, если старать  повысить надежность теста. Отбирая задания с большими коэф­фициентами интеркорреляции, можно обеспечить высокую од­нородность содержания и надежность теста. Это противоречие, получившее название «парадокс Ф.Лорда», приводит к возник­новению серьезных проблем при конструировании теста.

Таким образом, при конструировании гомогенного теста сле­дует стремиться к повышению в разумных пределах его надежно­сти, чтобы не снизить существенным образом содержательную валидность теста. Поэтому при отборе заданий в тест необходимо иметь четкое представление об их содержании и о множестве дру­гих факторов, а не просто отдавать предпочтение тем заданиям, которые высоко коррелируют друг с другом и обеспечивают хоро­шую надежность теста. По мнению Кэттела и Клайна, максимум валидности может быть получен тогда, когда все задания слабо, но положительно коррелируют друг с другом, однако каждое из них имеет высокую корреляцию с критерием по тесту [26]. Поэто­му повышению валидности способствует включение заданий, для которых характерны большие коэффициенты бисериальной кор­реляции с суммой баллов по тесту.

По рассматриваемой выше проблеме существует и другая точ­ка зрения. Так, Гилфорд и Ньюнелли |26] полагают, что внутрен­няя согласованность теста — непременное условие его высокой содержательной валидности, и потому высокая надежность явля­ется предпосылкой оптимальной валидности теста.

Количественные оценки валидностн. При количественных оцен­ках валидности для педагогических тестов в качестве критерия обычно берутся оценки экспертов, выставленные ими при тради­ционной проверке знаний учеников без использования тестов. Процесс валидизапии осложняется необходимостью установле­ния меры согласованности оценок экспертов, которых обычно бывает не менее трех человек. Если мера согласованности доста­точно высока, то для оценки валидности используется формула

где X_i - X — отклонение тестового балла i-го ученика от среднего балла по тесту; Х_mi –Х_э — отклонение балла i-гo ученика у экспер­тов от Х_э - среднего арифметического экспертных оценок; S²_x — дисперсия баллов учеников по тесту; S_mx² — дисперсия баллов т- го эксперта; т — число экспертов.

Бывают случаи, когда педагог заинтересован в оценке прогно­стической валидности, указывающей меру вероятности прогноза успешности дальнейшего обучения по результатам выполнения теста. В этом случае результаты по тесту коррелируют с результатами поступивших абитуриентов после окончания первого года обу­чения в вузе. Высокая корреляция означает, что разработанные тесты дли отбора абитуриентов в вуз прогностичны.

Источники повышения валидности теста. Для повышения со­держательной валидности теста необходимы:

- подбор оптимальной трудности заданий;

- экспертиза качества содержания теста;

- расчет оптимального времени выполнения теста;

- подбор валидных заданий с высокой дискриминативностью.