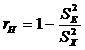|
Лекция 7. Педагогические измерения.
1. Компоненты и уровни измерений. 2. Объективность педагогических измерений. 3. Размерность пространства измерений, одномерные и многомерные конструкты, латентные переменные. 4. Уровни измерений в образовании. 5. Надежность и валидность результатов педагогических измерений.
Основные понятия теории педагогических измерений
Измерение в образовании, латентные переменные. Согласно наиболее распространенному определению, введенному в 1946 г. американским психологом С.Стивенсом, измерение – это процедура приписывания чисел некоторым характеристикам объектов в соответствии с определенными правилами [6; 22]. Данное определение – результат формального обобщения опыта количественных измерений, широко применяемых в физике и других естественных науках, однако на протяжении многих лет его брали за основу и в эмпирических науках. По мере развития педагогики, психологии и социологии возникла потребность во введении не только количественных, но и качественных оценок для величин, отличающихся по степени проявления того или иного свойства. Качественные оценки являются менее точными по сравнению с количественными в силу применяемых способов и инструментов измерения. Например, классифицирующие понятия в образовании («знающий», «подготовленный» и др.), которые дифференцируют обучающихся по уровню знаний и играют важную роль в учебном процессе, определяются субъективно учителем или группой учителей. Нередко качественные оценки выражают с помощью чисел, которые выбирают на основе экспертных суждений и соглашений. Приписываемые числа могут трактоваться по-разному. Так, в традиционном педагогическом контроле у каждого учителя есть свои представления о том, за что нужно ставить «5», «4», «3» и т.д. Неоднозначность оценивания в образовании усугубляется латентным (скрытым, исключающим возможность непосредственного измерения) характером измеряемых переменных. В силу латентности оцениванию подвергаются не сами характеристики обученности и обучаемости, а их эмпирические референты – наблюдаемые признаки измеряемых характеристик. Выбор последних происходит, интуитивно, поэтому их соответствие латентным характеристикам нуждается в доказательстве на основе экспертного и статистического анализа эмпирических результатов измерения. Современная трактовка понятия «педагогическое измерение». Современная теория измерений появилась в 80-х гг. XX в. Она строится на более строгой аксиоматической основе [22; 34]. В соответствии с новыми представлениями, измерение трактуется как конструирование числовой функции, осуществляющей изоморфное отображение некоторой эмпирической структуры в соответствующим образом подобранную числовую структуру. Изоморфизм – важное понятие математики, которое определяет ряд условий взаимно однозначного, отображения двух множеств с сохранением их свойств в процессе такого отображения. Хотя это понятие впервые появилось в высшей алгебре, в наше время оно используется довольно широко, хотя и не вполне строго, например в педагогических измерениях. Поскольку эмпирическая структура и строящаяся по результатам оценивания числовая структура (шкала) изоморфны, имея шкалу, можно, не обращаясь непосредственно к измеряемым объектам, восстановить все их свойства, характерные для эмпирической структуры. 1. Компоненты процесса педагогических измерений. Процесс педагогических измерений включает: - выбор предмета измерения (латентных характеристик объектов) и их числа; - выбор эмпирических референтов (наблюдаемых характеристик объектов); - выбор измерительных процедур; - конструирование и использование измерительных инструментов; - выбор шкалы (если измеряемая переменная одна) или шкал (если измеряют более одной переменной при многомерных измерениях); - построение отображения результатов измерения на шкалу (шкалы в случае многомерных измерений) по определенным процедурам и правилам; - обработку, анализ и интерпретацию результатов измерения. В силу неизбежности ошибок измерения оцениваемые характеристики объектов могут принимать более или менее точные значения, поэтому эти характеристики принято называть переменными измерения. Любые отклонения от стандартизированных условий измерения, обработки, анализа и интерпретации полученных результатов увеличивают ошибки измерения, которые представляют наибольшую опасность в эмпирических науках в силу латентного характера переменных. Поэтому так важен анализ устойчивости и точности (надежности) результатов тестирования, что выгодно отличает тесты от традиционных оценочных средств [22; 46; 60]. Еще одна характеристика качества результатов тестирования – валидность – отражает адекватность эмпирических результатов поставленным целям измерения [22; 60]. В силу многогранности целей анализ валидности должен быть многоаспектным, но в любом случае важное, место занимает доказательство адекватности эмпирических референтов концептуально выделенной переменной (переменных) измерения (конструктная валидность). Измерительный инструмент. Измерительный инструмент включает два компонента. Первый компонент – само измеряющее устройство, роль которого в педагогических измерениях чаще всего, но не всегда выполняет тест. В самом обобщенном виде под тестом можно понимать совокупность контрольных заданий в стандартизированной форме, обладающих необходимыми системообразующими статистическими характеристиками и обеспечивающих обоснованные оценки концептуально выделенной переменной (переменных) измерения с высокой объективностью. Таким образом, в самом определении теста заложены требования к его качеству, отсутствующие в традиционных оценочных средствах. Второй компонент измерительного инструмента – заранее подготовленная шкала, которая служит для фиксации результатов измерения и на которой откладываются оценки (количественные или качественные) измеряемой переменной. В процессе упорядочения оценок каждому элементу совокупности наблюдаемых эмпирических данных ставится в соответствие определенный балл, устанавливающий положение наблюдаемого элемента на шкале, где можно размещать сырые (первичные) баллы (результаты суммирования оценок по отдельным заданиям теста) или производные баллы, получающиеся в результате преобразования первичных оценок для повышения сопоставимости и удобства интерпретации результатов учащихся. Шкала с отложенными оценками переменной, является целью измерения. При измерениях с высокой надежностью, и валидностью она адекватно отображает оцениваемые характеристики и представляет их без существенных искажений. В зависимости от количества оцениваемых характеристик объекта можно говорить об одномерных (одна переменная) или многомерных (более одной переменной) измерениях. Соответственно по результатам измерения строился одна шкала или несколько шкал, число которых в последнем случае обычно бывает равно числу переменных измерения. Обработка и анализ данных измерения. Последний компонент процесса педагогических измерений, включающий обработку, анализ и интерпретацию данных, служит для выявления обеспечиваемого качества результатов измерения, коррекции тестов и представления полученных данных в форме, удобной для интерпретации и сравнения. Благодаря сопоставимости тестовых баллов, достигаемой в процессе обработки, по результатам педагогических измерений можно выстраивать качественный анализ результатов учащихся, проводить мониторинг и принимать обоснованные управленческие решения в образовании.
2. Объективность педагогических измерений
Может ли быть абсолютная объективность? Появление первых стандартизованных тестов в образовании вызвало массовую позитивную реакцию, поскольку первоначально они рассматривались как средство получения объективных оценок подготовленности обучаемых, преодолевающее субъективизм традиционных оценочных средств. По мере развития теории педагогических измерений и накопления опыта применения тестов пришло понимание того, что абсолютная объективность – это недостижимая характеристика результатов любых, в том числе и педагогических, измерений в силу существования ошибочных компонентов, неизбежно смещающих оценки. Поэтому при использовании тестов можно говорить лишь о высокой или низкой объективности, степень проявления которой связана с величиной надежности теста. Наиболее полно трактовка термина «объективность измерений» представлена в исследованиях Е.Вебстера (E.Webster) [22], предложившего восемь толкований этого понятия. Три из них – процедурная объективность, классическая (традиционная) объективность и инвариантная (специфическая) объективность – непосредственно относятся к педагогическим измерениям. Процедурная объективность. Под процедурной объективностью (первая трактовка термина «объективность измерений») понимается независимость результатов тестирования от субъективных суждений педагога, использующего тест. Эта независимость обеспечивается благодаря равенству условий тестирования, использованию для одной группы тестируемых параллельных (совпадающих по трудности и другим характеристикам) вариантов теста, стандартизации процедуры проверки результатов и максимальной ее автоматизации, исключающей влияние педагога на оценки. Сведение всех видов объективности только к процедурной недопустимо, поскольку при таком подходе не выдвигается никаких требований к качеству теста. В этом случае может создаться впечатление, что для получения объективных данных о подготовленности испытуемых достаточно перейти от традиционных экзаменов к любым, в том числе некачественным, тестам, устранив влияние педагога на оценку тестирования путем автоматизации процедуры подсчета баллов испытуемых. Классическая, или традиционная, объективность. Второе, углубленное, понимание объективности измерений рассматривается в классической теории тестов и основывается на понятиях «сырой балл» и «истинный балл», отличающихся друг от друга на величину ошибки измерения. Сырой (первичный, наблюдаемый, индивидуальный) балл получается простым суммированием результатов испытуемого по отдельным заданиям теста. При дихотомической оценке результатов по заданиям (1 или 0) индивидуальный балл равен количеству правильно выполненных заданий теста. Истинный балл в классической теории отождествляется с абсолютно объективной оценкой свойств испытуемого, свободной от влияния любых ошибок измерения. В отличие от сырого балла, который меняется в зависимости от теста и способа подсчета результата испытуемого, истинный балл трактуется как не зависящая от средств измерения константа, характеризующая оцениваемое свойство испытуемого в момент измерения, но меняющаяся в процессе обучения. Согласно основной аксиоме классической теории тестов любой наблюдаемый балл равен сумме истинного балла и ошибки измерения. В тех случаях, когда ошибка измерения не превышает выбранных пределов точности измерений, говорят о высокой объективности результатов тестирования, а оценки испытуемых принимают за их истинные баллы. Таким образом, углубленное понимание объективности измерений требует оценивания величины ошибки измерения, на размер которой влияют не только условия проведения тестирования, но и качество теста. Инвариантная, или специфическая, объективность. Третья трактовка объективности основана на современной теории конструирования тестов – Item Response Theory (IRT). Преимущества.IRT, позволяющие оценить подготовленность обучаемых независимо от трудности заданий теста, приводят к достижению так называемой инвариантной объективности измерений, которая предпочтительнее объективности, обеспечиваемой классической теорией тестов [60]. Для достижения специфической объективности необходима подгонка данных тестирования к требованиям моделей теории IRT и длительная серьезная работа над тестом. Поэтому на практике тестологи часто сталкиваются с тем, что эффект инвариантной объективности либо реализуется со слишком большими затратами, либо не реализуется вообще в силу недостаточно высокого качества теста.
3. Размерность пространства измерений, одномерные и многомерные конструкты, латентные переменные.
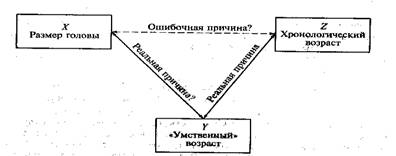
Концептуальные и реальные переменные измерения, конструкты. Измерение начинается с постановки цели, в соответствии с которой выбирают одну (одномерный случай) или несколько (многомерный случай) переменных. В последнем случае для обозначения измеряемых характеристик часто используют обобщающий термин – «конструкт». Каждый разработчик теста уверен в том, что он ясно представляет себе измеряемые характеристики и способен на основании своего педагогического опыта точно подобрать задания обеспечивающие оценивание конструкта. Многие тестологи так и остаются в полном заблуждении относительно того, что на самом деле измеряет тест, поскольку не проверяют соответствие задуманного конструкта и реальных результатов измерения. Анализ такого соответствия является необходимым этапом оценивания валидности измерения. Нередко его пытаются провести априорно, до начала тестирования, экспертным путем, и в результате, как правило, получают недостоверную информацию. Для корректного оценивания валидности необходим статистический анализ эмпирических данных тестирования, поэтому понять, что же мы на самом деле измеряем, можно лишь после применения теста. Сложность процедуры установления размерности пространства измерений увеличивает проблемы, связанные с неоднозначной трактовкой многих конструктов в образовании и в других социальных науках (рис. 2). Каждый педагог вкладывает в оценивание учебных достижений свое видение оптимального набора переменных измерения. Неоднозначность трактовки конструкта усугубляется по мере продвижения от начальных ступеней образования к более высоким ступеням, когда содержание большинства учебных курсов приобретает междисциплинарный характер.
Рис. 2. Пример неоднозначной трактовки конструкта и ошибки в выводах о связи переменных
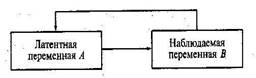
Операционализации. Операционализация заключается в придании оцениваемым латентным характеристикам подготовленности учащихся формы, удобной для фиксации определенными правилами измерения. При педагогическом измерении в качестве таких характеристик подготовленности обучаемых обычно выступают знания, умения, навыки, компетентности и т.д. ... В процессе операционализации происходит выделение, набора эмпирических индикаторов, в роли которых выступают задания теста. Количество правильно выполненных заданий, подсчитанное и преобразованное по определенным правилам, дает основание для присвоения испытуемому определенного места на шкале переменной измерения. Визуализация результатов педагогического измерения. Визуализация – геометрическая интерпретация связи между латентной переменной А (одномерной или многомерной) и наблюдаемой переменной В – показана на рис. 3.
Рис. 3. Связь между латентной и наблюдаемой переменными.
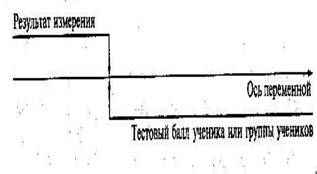
Стрелки на рисунке указывают характер связи между переменными. Латентная переменная А является первопричиной, порождающей множество наблюдаемых результатов выполнения теста. Однако при измерениях всегда ставят обратную задачу – по наблюдаемым результатам тестирования найти достаточно точные оценки латентных переменных. Взаимосвязь результатов измерения и положения испытуемого на шкале переменной для одномерного случая представлена на рис. 4. Каждая оценка переменной измерения для учащихся из тестируемой группы соответствует одной из точек оси. В свою очередь каждая точка определяет положение испытуемого или группы испытуемых с одинаковым тестовым баллом, полученным по результатам выполнения теста.
Рис. 4. Геометрическая интерпретация результата тестовых измерений
На изображенной оси более высокие баллы располагаются правее, а более низкие – левее. Крайний слева результат отражает случай, когда испытуемый выполнил правильно лишь несколько заданий теста. Противоположной ситуаций, когда ученик выполнил все или почти все, соответствует крайняя правая точка на оси переменной измерения. Остальные точки занимают некоторое промежуточное положение на отрезке, где лежат тестовые баллы учащихся. Если правильно выполненные задания теста соотнести с результатами учащихся и расположить их вдоль оси переменной измерения, то можно предположить, что более трудны задания сместятся вдоль оси вправо, так как их, скорее всего, будут выполнять правильно наиболее сильные учащиеся в классе. И наоборот, более легкие задания будут смещены влево – они по силам ученикам с низким уровнем подготовки (см. рис. 5).
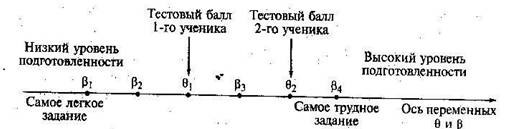
Рис. 5. Соотношение между трудностью заданий и подготовленностью учащихся: β– уровень трудности j -го задания, j = 1, 2,.... 4, θ1 и θ2 – тестовые баллы двух учащихся
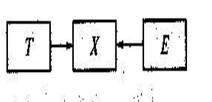
Из дидактических соображений на рисунке показано выполнение четырех заданий, однако все выводы, получаемые с помощью этого примера, применимы к любому числу заданий в тесте. Расположение тестового балла первого учащегося говорит о том, что он выполнил верно два самых легких задания, но не справился с третьим и четвертым заданиями. Второй учащийся имеет более высокий тестовый балл и подготовлен лучше. Он не выполнил только самое трудное – четвертое задание теста. Ошибки измерения. Локализация места расположения результата ученика на оси переменной зависит в основном от соотношения между величиной его истинного балла и трудностью заданий теста. Если балл довольно высок, а задание довольно легкое, то у ученика все основания для успешного выполнения этого задания теста. В противном случае ученика скорее всего ждет неудача. Конечно, наверняка предугадать ничего нельзя в силу действия различных смещающих факторов (эффект забывания, подсказки и т.д.), поэтому обычно говорят лишь о некоторой вероятности успеха или неуспеха. Вероятностный характер наблюдаемых результатов выполнения теста Обусловлен влиянием случайных и неслучайных ошибок измерения. В число последних входят те, которые появляются из-за просчетов разработчиков в процессе создания теста. К ошибкам систематического характера могут также привести нарушение требований к сбору статистических данных, некачественная интерпретация результатов выполнения теста и ряд других причин. К случайным факторам можно отнести настроение испытуемого, поведение экзаменатора, обстановку при тестировании в классе и многое другое – словом, все, что учесть и предвидеть при тестировании попросту невозможно. Одномерные измерения. Чаще всего при планировании измерений в образовании выбирают одномерные конструкты. Это упрощает процесс построения шкалы, но не всегда бывает адекватно содержанию тестов. Рис. 6 иллюстрирует случай одномерных измерений, который может быть интерпретирован следующим образом: одна латентная переменная Т – истинный уровень подготовленности каждого обучаемого – приводит к возникновению одной оценки наблюдаемой переменной Х – уровня подготовленности обучаемого. Помимо переменной Т на оценку X оказывает влияние фактор Е – ошибка измерения.
Рис. 6. Иллюстрация связи переменной измерения, истинного бала и ошибки при одномерном измерении
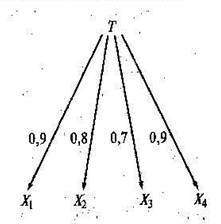
Чтобы принять гипотезу об одномерности теста, необходимо выявить связь между теоретическим конструктом и эмпирическими индикаторами, роль которых выполняют задания теста. Оценка связи требует ответа на вопрос – есть ли разница между доказательством одномерности конструкта и доказательством одномерности заданий теста? На рис. 7 представлена измерительная модель для одномерного случая, иллюстрирующая связь между конструктом, обозначенным символом Т, и четырьмя заданиями (Х1, Х2, Х3, Х4), Числа, стоящие у каждого луча, показывают меру предполагаемой корреляционной связи между конструктом и эмпирическими индикаторами – заданиями теста.
Рис. 7. Измерительная модель, иллюстрирующая связь между конструктом и заданиями теста (одномерный случай)
При анализе модели важно понимать, что конструкт является латентным (скрытым от возможностей непосредственного измерения) фактором, взаимодействие которого с заданиями порождает наблюдаемые результаты выполнения теста. Влияние конструкта на наблюдаемые переменные показано на рис. 7 с помощью направленных лучей. Поскольку каждое задание в рассмотренном гипотетическом примере измеряет только один конструкт, то справедлив, вывод об одномерности заданий теста. Обратный вывод, в общем случае, неверен: из одномерности заданий не следует одномерности теста. Многомерные измерения. Если конструкт включает не одну, а несколько переменных, то измерения называются многомерными, Совокупность переменных образует пространство переменных измерения, размерность которого равна их числу. Иногда при проведении многомерных измерений создают несколько субтестов, каждый из которых является одномерным и измеряет свою переменную с помощью одномерных заданий. Примером такого подхода является полидисциплинарный тест, состоящий из набора одномерных субтестов. В другом случае в многомерных измерениях используют междисциплинарный тест, задания которого не являются одномерными. Каждое из заданий измеряет свою совокупность переменных, которые могут отличаться как по количеству, так и по содержательной трактовке конструкта. В практике педагогических измерений существуют специальные методы анализа размерности пространства измерений. Такую группу методов предоставляет исследовательский и конфирматорный факторный анализ, применение аппарата которого основано на использовании соответствующего программного обеспечения, например статистического пакета SPSS.
4. Уровни измерений в образовании
Типология уровней измерения. Общая типология уровней измерения основывается на проявлении совокупности свойств, лежащей в основе построения шкал. В качестве таких свойств выделяют: идентичность, позволяющую однозначно относить объекты к одной из выделяемых совокупностей; транзитивность, способствующую ранжированию объектов в определенном порядке; метричность, обеспечивающую единую единицу измерения, и наличие абсолютного нуля. Наиболее общая классификация, предложенная С.Стивенсон [18; 22; 60], включает четыре уровня измерений и фиксирует присущие им свойства. Согласно такой классификации различают шкалы качественные (шкала наименований, или классификаций, и порядковая шкала) и количественные (интервальная шкала и шкала отношений) шкалы. Качественные шкалы иногда называют неметрическими (концептуальными), а количественные – метрическими (материальными). Для каждого уровня измерений существуют группы допустимых преобразований и операций с различными математическими и статистическими величинами, характеризующими измеряемые признаки. Качественные шкалы. На качественном уровне отнесение эмпирических объектов измерения к различным классам проводится по признаку эквивалентности (шкала наименований, или номинальная шкала) или по признаку упорядочения внутри эквивалентных объектов одного класса (порядковая шкала). Для построения шкалы наименований и порядковой шкалы в основном применяются экспертные методы, при которых оценки на шкале считаются достоверными, если они признаны большинством экспертов, Примером номинальной шкалы могут служить результаты зачетной сессии, когда все студенты делятся на две труппы – получивших и не получивших зачет. Порядковые шкалы используются в образовании в тех случаях, когда педагогический контроль осуществляется традиционными способами без применения тестов. Например, порядковой является привычная четырехбальная школьная шкала, которую иногда неоправданно называют пятибалльной. Каждой группе учащихся, проявляющей согласно мнению, учителя сходные знания, присваивается одинаковый (один из четырех) номер места от двух до пяти. Недостатки качественных шкал – ограниченная сфера применения и низкая точность измерения. Числа или символы, приписываемые объектам путем экспертного оценивания, субъективны и носят исключительно условный характер. Их нельзя суммировать или проводить с ними другие математические операции. Количественные шкалы. К количественным шкалам относятся интервальная шкала и шкала отношений. Процесс их построения основывается на измерениях, поэтому представленные в них оценки характеристик объектов отличаются более высокой объективностью по сравнению с оценками в качественных шкалах и поддаются определенным математическим операциям. Интервальная шкала используется для упорядочения объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. В ней определено расстояние между объектами и предусмотрена общая для всех объектов единица измерения, а началом отсчета является условно выбранная нулевая точка. Благодаря существованию единицы измерения в интервальной шкале возможны все арифметические действия над числами, кроме операции деления в силу отсутствия абсолютного нуля. Примером интервальной шкалы в образовании, обеспечивающей корректную сравнимость результатов педагогических измерений, является шкала логитов, построение которой осуществляется на основе теории IRT [22; 60; 67; 83]. Шкала отношений описывает свойства объектов, удовлетворяющие отношениям эквивалентности, порядка, аддитивности и пропорциональности. Последнее свойство появляется благодаря существованию в этой шкале однозначного естественно определенного критерия нулевого проявления измеряемого свойства – абсолютного нуля. Другими словами, шкала отношений является интервальной шкалой с естественным, а не условным началом отсчета, что расширяет возможности преобразований чисел, приписанных объектам. По сравнению со всеми ранее рассмотренными шкалами эта шкала обеспечивает самый высокий уровень измерений, но реализовать ее в образовании невозможно в силу отсутствия абсолютного нуля.
5. Надежность и валидность результатов педагогических измерений
Общие замечания. Размерность, надежность и валидность являются взаимосвязанными свойствами, характеризующими различные аспекты качества педагогических измерений. Выявление размерности – необходимый предварительный этап работ по оцениванию надежности и валидности результатов измерений. Надежность результатов тестирования. Надежностью (reliability) называется характеристика точности тестовых результатов и их устойчивости к действию случайных факторов [60]. По сложившейся традиции термин «надежность» часто, хотя и не совсем верно, используют по отношению к тесту. Однако надежность теста является необходимым, но не достаточным условием получения высокой точности измерений. В случае нарушений требований к стандартизации условий проведения тестирования, проверке и оцениванию его результатов даже с помощью очень надежного измерителя можно получить результаты со значительным ошибочным компонентом. Концепция истинного балла. Анализ надежности основан на предположении классической теории тестов о связи между наблюдаемым баллом, истинным баллом и ошибкой измерения. Оценка истинных баллов (true scores) испытуемых – главная цель всех, кто создает или применяет педагогические тесты. Так как любые результаты тестирования всегда содержат в себе ошибочные компоненты, то приходится заменять истинные баллы – параметры испытуемых – их наиболее достоверными оценками, которые тем точнее, чем надежнее тест.
Концептуальная формула для
коэффициента надежности.
Основная аксиома классической теории тестов приводит к
фундаментальному соотношению, позволяющему получить концептуальную
формулу для коэффициента надежности результатов измерений
(количественной характеристики надежности), которая связывает
дисперсию (показатель разброса) наблюдаемых баллов
Ее значение исключительно теоретическое,
поскольку по эмпирическим результатам выполнения теста нельзя
подсчитать
Несложный анализ формулы для
оценивая надежности (1) позволяет сделать выводы о возможных
пределах величины rн.
Очевидно, что дробь
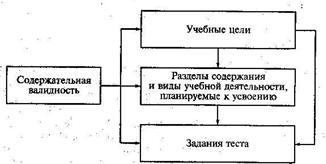
Факторы, влияющие на надежность гомогенного теста. На основе постулатов классической теорий тестов и различных модификаций концептуальной формулы (1) можно определить факторы, влияющие на повышение надежности теста. 1. Если при компоновке теста отбирать задания, имеющие наибольшую корреляцию с другими заданиями теста, то тест будет иметь высокую надежность и обеспечит низкую погрешность измерения. Другими словами, чем выше содержательная однородность (гомогенность) теста, тем он надежнее. Этот вывод представляет особую важность для коротких тестов (от 20 до 35 заданий). В очень длинных тестах (более 100 заданий) малые значения интеркорреляции заданий могут сочетаться с высокой надежностью теста. 2. Надежность измерений повышается с увеличением длины теста. Этот формальный вывод не всегда согласуется с реальными возможностями учеников. По мере роста длины теста повышается утомляемость и снижается мотивация к выполнению заданий, что в совокупности ведет к росту ошибки измерения. Поэтому при выборе оптимальной длины теста разработчики анализируют группу факторов, среди которых: высокая дисперсия тестовых баллов, нормальный характер их распределения, форма используемых заданий, возраст учеников и время выполнения теста, выбранное в соответствии с целями тестирования и физиологическими возможностями учащихся. По данным Н.Гронлунда, учащиеся старших классов в среднем за 1 мин могут выполнить одно задание с выбором ответа (при числе ответов не более четырех) [88]. На задание с кратким дополняемым ответом требуется в среднем до 2 мин, а с полным свободно конструируемым ответом – до 5 мин. В целом для обеспечения достаточно высокой надежности измерений рекомендуется проводить тестирование выпускников неполной средней школы (IX класс) в течение 2 – 3 уроков, а выпускников средней школы (XI класс) – в течение 2—4 уроков. Валидность результатов педагогических измерений. Валидность – это характеристика адекватности результатов измерения поставленной цели создания теста [60]. Другими словами, валидность – это характеристика того, в какой мере удается измерить именно запланированный конструкт. Поэтому оценивание валидности тесно связано с анализом размерности пространства педагогических измерений. Оценивание валидности. Количественная опенка валидности получается путем соотнесения результатов измерения с различными внешними критериями (обычно качественного характера), независимо описывающими вне ситуации тестирования все, что собирались измерять. Высокая корреляция результатов измерений с внешними критериями свидетельствует о высокой валидности теста. Наоборот, слабая корреляция указывает на неполную адекватность теста своему предназначению и позволяет сделать вывод о низкой валидности теста. Поскольку можно выбрать достаточно много внешних критериев адекватности теста поставленным целям измерения, существуют различные виды валидности и многочисленные методы ее исследования. Конструктная валидность. Оценка конструктной валидности связана с выявлением того, насколько хорошо измеряется концептуально выбранный латентный конструкт. При анализе конструктной валидности часто рассматривают корреляцию между результатами по новым и уже существующим тестам, валидность которых подтверждена многолетней практикой их применения. Проводят независимую экспертизу качества содержания теста, используют факторный анализ, позволяющий выстроить факторную структуру теста, анализируют внутреннюю согласованность теста методами корреляционного анализа и т.д. Содержательная валидность. В педагогических измерениях на первый план выходит исследование содержательной валидности теста, основанное на тщательной экспертизе. В общем случае содержательная валидность – это степень релевантности и репрезентативности отражения концептуально выделенного конструкта в содержании заданий теста. В основе работы экспертов обычно лежит анализ полноты, значимости, правильности пропорций содержания теста и его соответствия запланированным для проверки видам учебной деятельности (рис. 8).
Рис. 8. Модель обеспечения содержательной валидности измерения
|