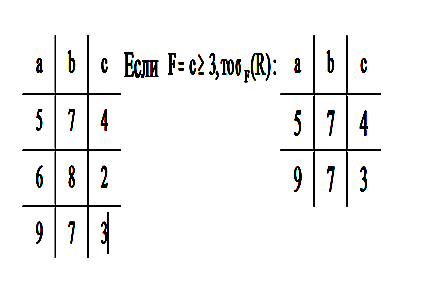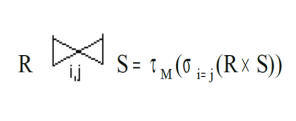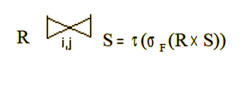|
4.3.1. Реляционная алгебра Рассмотрим операции реляционной алгебры, для каждой введём обозначе- ние и мнемоническую запись, удобную для использования в ЯМД. A) Теоретико-множественные операции. Прежде всего к этим операциям относят объединение, пересечение и раз- ность, понимаемые также, как в теории множеств (см. [32]). При этом накладыва- ются ограничения на операнды – они должны быть однотипными, т.е. иметь оди- наковый набор атрибутов. Обозначения операций соответственно - È ,Ç , / .{UNION|MINUS|NTERSECT }<параметры> - мнемоническая записьопераций. К этой группе операций относят и п роизведение (фактически обобщениедекартового произведения).
где || - склейка кортежа MULTIPLE <параметры> – мнемоническая запись. B) Операция проекции
PROJECT <отношение> OVER <атрибуты> – мнемоническая запись. |
|
C) Операция селекции
Пусть F – формула, образованная операндами, являющимися атрибутами от- ношений или константами, а также логическими связками. Тогда,
мула F. Пример.
|
|
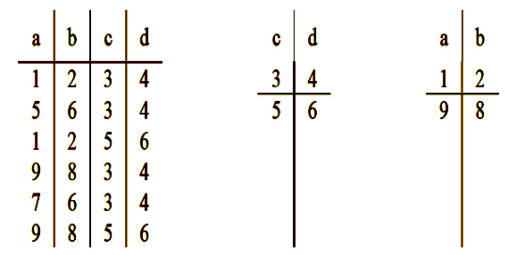
SELECT <отношение> WHERE <формула> – мнемоническая запись D) Деление R ¸ S={t}, где t – подкортеж длины r-s, такой что "u Î S, t || uÎ R.Пример.
DIVIDE <параметры> - мнемоническая запись. |
|
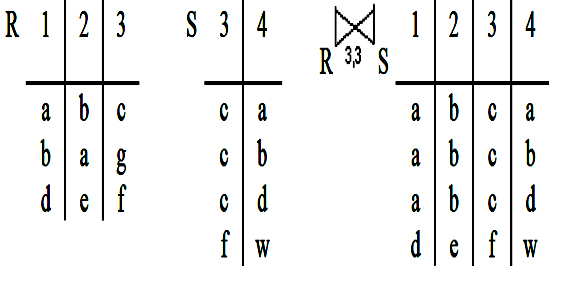
E) Соединение (операция дополнительная). – операция соединения по i-му атрибуту отношения R и j-му атрибуту отношения S. M – множество всех атрибутов отношений R и S за исключением j-го атрибута отношения S (атрибут исключается во избежание бесполезного дублирования).
Возможна операция соединения по произвольному условию. В этом случае оно определяется как применение селекции по заданному условию к произведению. |
|
JOIN <отношение 1, отношение 2> ON {<атрибуты>|<условие>} На основе операций реляционной алгебры, определен готовый язык манипулирования данными, к нему требуется лишь добавить команды действий над выбранными данными, например OUTPUT и DELETE. Пример запроса 1. <2 лет. |
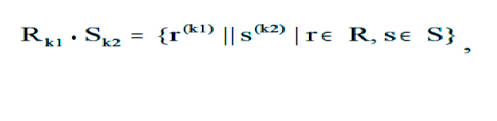
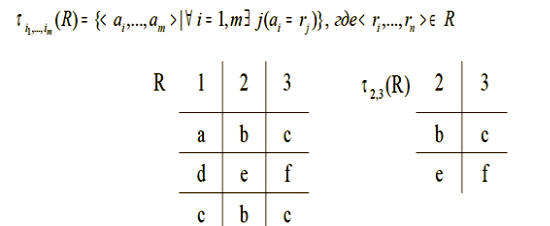
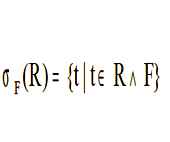 –
множество кортежей отношения R, для которых истинна фор-
–
множество кортежей отношения R, для которых истинна фор-