|
6.5.2. B-дерево Для улучшения характеристик поиска
целесообразно строить разреженный индекс для разреженного индекса,
для которого в свою очередь также строить разреженный индекс и т.д.
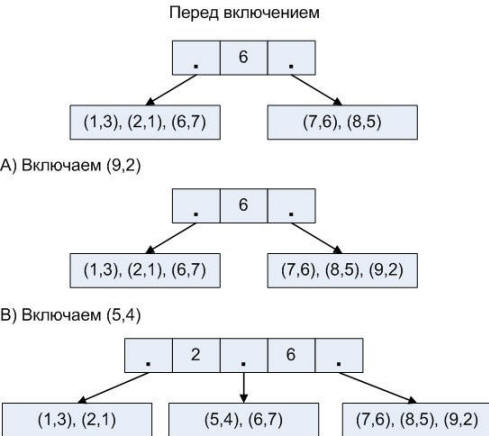
Таким образом, можно добиться, чтобы разреженный Рис. 26. Включение в разреженный индекс |
|
Вставка элемента в B-дерево и удаление из B-дерева предполагают соответственно вставку в разреженный индекс и удаление из разреженного индекса низшего уровня, при этом может потребоваться коррекция индекса более высокого уровня (в случае нарушения условий) и т.д.
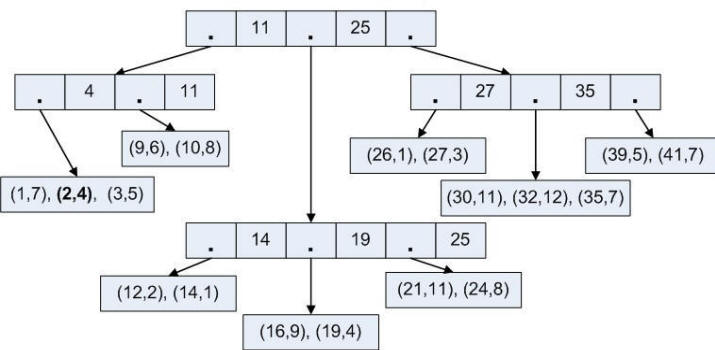
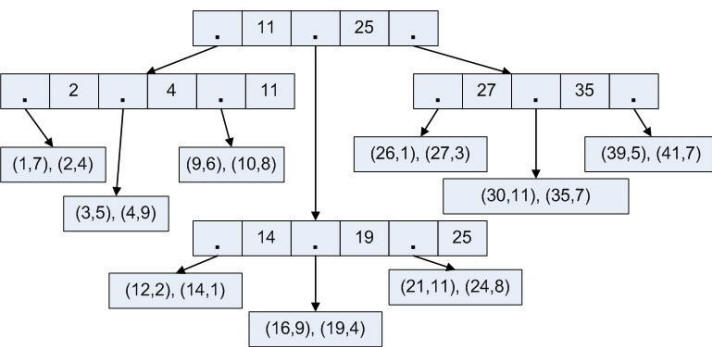
Рис. 27. B-дерево |
|
Рассмотрим примеры. Рис. 28. Вставка в B-дерево |
|
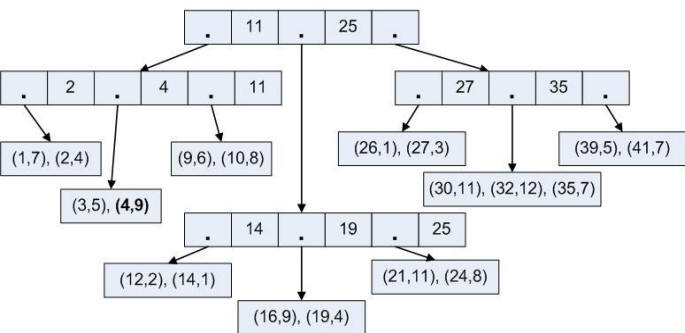
B) Вставим теперь элемент (4,9) (рис.
29) Рис. 29. Вставка в B-дерево |
|
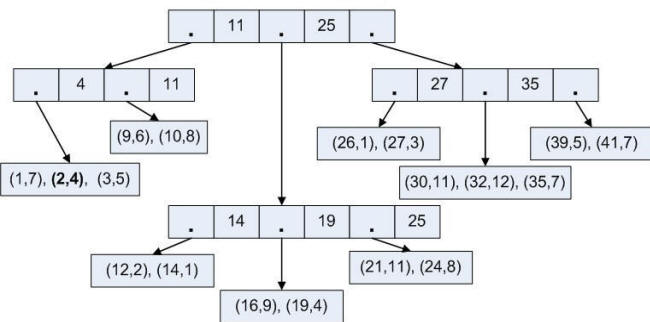
C) Удалим элемент (32,12) (рис. 30)
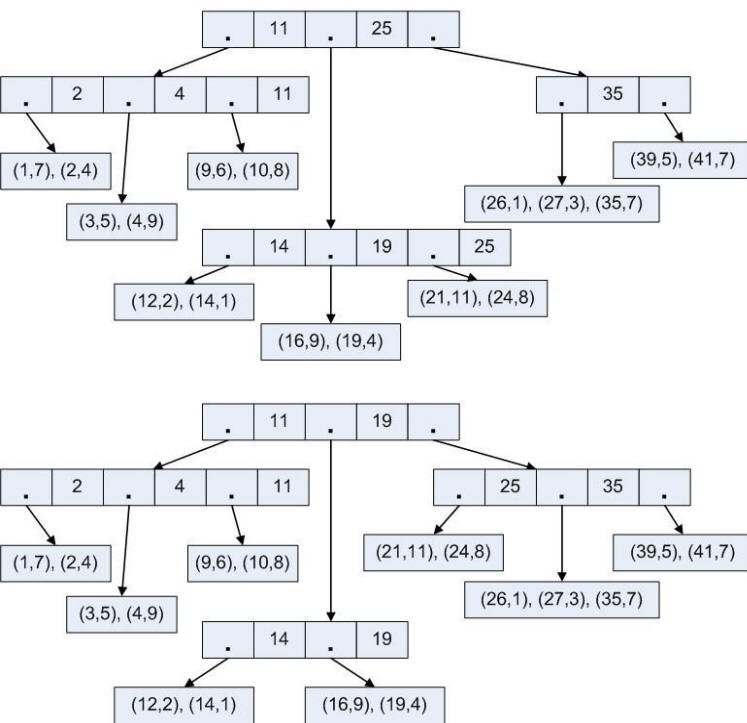
Рис. 30. Удаление из B-дерева |
|
D) Удалим элемент (30, 11) (рис.
31)
Рис. 31. Удаление из B-дерева
|