Технология решения задач на ЭВМ
Основные этапы
Решение задач с помощью компьютера включает в себя следующие основные этапы,
часть из которых осуществляется без участия компьютера.
1) Постановка задачи:
сбор информации о задаче;
фоpмулиpовка условия задачи;
определение конечных целей pешения задачи;
определение формы выдачи результатов;
описание данных (их типов, диапазонов величин, структуры и т.п. ).
2) Анализ и исследование задачи, модели:
анализ существующих аналогов;
анализ технических и программных средств;
pазpаботка математической модели;
разработка структур данных.
3) Разработка алгоритма:
выбор метода проектирования алгоритма;
выбор формы записи алгоритма (блок-схемы, псевдокод и др.);
выбоp тестов и метода тестиpования;
проектирование алгоритма.
4) Пpогpаммиpование:
выбор языка программирования;
уточнение способов организации данных;
запись алгоpитма на выбpанном языке пpогpаммиpования.
5) Тестиpование и отладка:
синтаксическая отладка;
отладка семантики и логической стpуктуpы;
тестовые pасчеты и анализ pезультатов тестиpования;
совершенствование пpогpаммы.
6) Анализ результатов решения задачи и уточнение в случае необходимости
математической модели с повторным выполнением этапов 2‑5.
7) Сопровождение программы:
доработка программы для решения конкретных задач;
составление документации к pешенной задаче, к математической модели, к
алгоритму, к пpогpамме, к набору тестов, к использованию.
Моделирование
Модели как специфическое средство и форма научного знания известны с давних
времен. Достаточно указать на представления Демокрита и Эпикура об атомах,
Птолемея о геоцентрической, а Коперника о гелиоцентрической моделях Вселенной.
Прослеживая историческое развитие научных идей и методов, можно заметить, что
модели постоянно создавались и создаются.
Предметом научного изучения модель стала не так давно. Поскольку модель стала
осмысливаться как инструмент изучения различных явлений действительности, то ею
заинтересовалась отрасль философии, которая носит название гносеологии.
Философия рассматривает сущность модели, ее функции в процессе познания.
Расцвет изучения и использования моделей приходится на XX век. Это не случайно.
Именно в прошлом веке наука достигла такого уровня развития, когда стали изучать
объекты высокой степени абстракции и обобщения, сложные и малодоступные системы.
И именно модели и метод моделирования позволяют проводить исследования в
ситуациях, когда изучение непосредственно самого объекта невозможно,
затруднительно, дорого, слишком длительно во времени и т. п.
Несомненно, что в наступившем веке модели будут играть еще большее значение, как
в науке, так и в различных областях практической деятельности. И не в последнюю
очередь это связано с дальнейшим развитием и внедрением
электронно-вычислительной техники во все области жизни современного общества.
Понятие моделирования сегодня имеет статус общенаучного понятия, имеющего
глубокий философский смысл. Моделирование как процесс построения и изучения
различных объектов посредством их моделей стало предметом философского познания
сравнительно недавно. В философской литературе широко обсуждаются
гносеологические и методологические аспекты моделирования. В частности, с точки
зрения философии осмысление вопроса о единстве мира осуществляется посредством
осознания аналогичности моделей (дифференциальных уравнений, функций и т. д.),
относящихся к разным областям мира. С гносеологической точки зрения этот вывод
очень важен, так как позволяет обнаружить и понять сущность связей внешне
отличающихся явлений.
Моделирование является одним из показателей процесса интеграции в современной
науке. Благодаря моделированию возникают более тесные связи между различными
науками.
МОДЕЛИ И МОДЕЛИРОВАНИЕ
Под моделью в различных областях человеческой деятельности понимают разное. Так,
говорят о моделях обуви, одежды, технических сооружений, атома, Вселенной и т.
д. Из анализа научной литературы можно заметить, что термин модель употребляется
в двух различных значениях:
некоторой теории,
описания, отражения некоторой теории.
Слово модель в переводе с латинского (modus, modulus) означает мера, образ,
способ и т. д.
В математических науках моделью принято обозначать теорию, которая обладает
структурным подобием по отношению к другой теории. Две такие теории называются
изоморфными, и одна из них выступает как модель другой и наоборот.
В естественных науках, таких, как физика, химия, биология и другие, термин
модель употребляется в другом смысле, не для обозначения теории, а для
обозначения того, что она описывает. Здесь с термином модель связаны два
значения. Во-первых, модель выступает как некоторая идеализация, упрощение
действительности. Например, в физике и химии используют модели атомов различных
веществ. Во-вторых, в более узком смысле, термин модель применяют для
обозначения физической аналогии, как отношение сходства систем, состоящих из
элементов разной физической природы, но обладающих одинаковой структурой.
Например, в химии используют кристаллические решетки как модели структуры
вещества.
Приведенные объяснения термина модель наиболее широко используются в научной
литературе. Существуют и другие толкования модели. В настоящее время из многих
определений модели наиболее употребительным является определение В.А. Штоффа, в
котором под моделью понимается такая мыслимо представимая или материально
реализованная система, которая, отображая или воспроизводя объект исследования,
способна замещать его так, что ее изучение дает новую информацию об этом
объекте. Из этого определения следует, что моделирование – это такой способ
исследования, когда изучение реальной системы заменяется изучением ее модели, а
затем полученные результаты распространяются на изучаемую систему. Это хорошо
прослеживается на примере истории открытия позитрона П. Дираком и нейтрино Э.
Ферми.
В 20-х годах XX века, исследуя уравнения квантовой механики, П. Дирак обнаружил
решение уравнения, которое характеризовало некоторую гипотетическую элементарную
частицу. Через несколько лет была экспериментально обнаружена эта гипотетическая
частица, названная впоследствии позитроном. Аналогичным образом Э. Ферми
предсказал существование элементарной частицы нейтрино, которая была
экспериментально обнаружена через 30 лет.
Моделирование основывается на методе аналогии, который позволяет установить
отношения изоморфизма между двумя объектами, каждый из которых может быть
абстрактным или реально существующим.
В естественных науках модель и теория по существу отличаются друг от друга. Под
теорией понимается совокупность утверждений об общих законах данной предметной
области, а под моделью – либо конкретный образ изучаемого объекта, либо какой-то
другой реально существующий объект и сходный с ним в отношении некоторых
структурных свойств. Следовательно, модель это то, что описывается данной
теорией, – своеобразный предмет данной теории.
Именно такой подход используется в информатике для раскрытия содержания модели.
Здесь модель понимается как заместитель изучаемого объекта, сходный с ним в
существенных свойствах и структуре. Это специфическая форма познания,
качественно отличающаяся от теории, гипотезы, так же как и от чувственного
образа.
КЛАССИФИКАЦИЯ НАУЧНЫХ МОДЕЛЕЙ
В основе общепризнанной классификации научных моделей лежит материалистическое
понимание модели как средства отображения, воспроизведения той или иной части
действительности с целью ее более глубокого познания.
Отношение между моделью и оригиналом, которое является отношением отражения или
воспроизведения, варьируется в зависимости от способа построения модели, т.е. от
тех средств, при помощи которых строится модель.
Так, в зависимости от способа построения моделей, от средств, какими
производится моделирование изучаемых объектов, все модели могут быть разделены
на два класса:
1) материальные (вещественные, реальные);
2) идеальные (мысленные, воображаемые).
К первому классу относятся модели, которые существуют объективно и воплощены в
материальных предметах, изготовленных из различных материалов (дерева, стекла,
металла и др.). Например, деревянные модели судов, металлические модели молекул
и т.д. Сюда же относятся и так называемые живые модели, которые отобраны
человеком в силу присущих им свойств, позволяющих в упрошенной форме имитировать
изучаемый сложный процесс. Например, в опытах физиологи используют специально
выведенные породы (или как их называют в биологической науке, линии) крыс:
Вистар, Аоки, Ока-мото и др.
Материальные модели, в свою очередь, могут быть разделены на три основные
группы:
1) пространственно подобные,
2) физически подобные,
3) математически подобные.
Первая группа представляет собой сооружения, создаваемые для воспроизведения или
отображения пространственных свойств или отношений объекта. Отношение этих
моделей к объекту характеризуется геометрическим подобием как обязательным
условием. К этой группе относятся макеты зданий, пространственные модели
кристаллов и молекул. Например, пространственная модель ДНК, построенная Ф.
Криком и Д.Уотсоном в 1953 году, представляет собой пространственную
спиралевидную конструкцию, составленную из специфически спаренных оснований –
аденина, тимина, гуанина и цитозина.
Вторая группа состоит из моделей, созданных для воспроизведения динамики
изучаемых процессов, различного рода зависимостей и закономерных связей,
структуры и других характеристик изучаемых явлений. Основой модельного отношения
здесь является физическое подобие модели и объекта, предполагающее одинаковость
или сходство их физической природы и тождественность законов движения. Например,
в кораблестроении, прежде чем строить корабль, строят его модель, которую
испытывают в бассейне, и по ходовым характеристикам модели определяют довольно
точно такие величины, как максимально допустимый крен корабля, его скорость при
разных режимах и другие характеристики. В генетике в качестве модели для
исследования проблем наследственности используют насекомое дрозофилу, ввиду
большой скорости ее размножения.
К третьей группе относятся системы, не обладающие с объектом одной и той же
физической природой и не сохраняющие с ним физического и геометрического
подобия. Здесь отношением между моделью и реальным объектом выступает аналогия.
Эта аналогия может быть структурной и функциональной, что находит свое выражение
в наличии одинакового математического формализма, которым описывается поведение
этих систем. Поэтому эти модели называются математическими. К ним относятся
аналоговые модели (например, электрические модели механических, биологических и
прочих явлений), структурные, цифровые и различные кибернетические
функциональные модели.
Процесс построения математических моделей реально функционирующих систем очень
сложен. Построение такой модели оценивается как выдающееся открытие. Так, в 1952
г. англичане Ходжкин А.Л. и Хаксли Э.Ф. построили математическую модель,
имитирующую распространение нервного импульса в живом организме. За это
достижение они были удостоены Нобелевской премии в 1963 году. Предложенная
модель представляет собой систему дифференциальных уравнений, описывающих
распространение нервного импульса. При этом оказалось, что модельные расчеты и
полученные экспериментальные данные хорошо согласуются. Важность построенной
модели для развития науки состояла в том, что, исходя из небольшого количества
экспериментальных данных, оказалось возможным объяснить с единой позиции ряд
явлений, которые ранее казались независимыми, а также предсказать новые. Вообще
ценность модели состоит в том, что она описывает большой круг явлений на
основании небольшого количества экспериментальных данных.
Материальные модели неразрывно связаны с идеальными. Последние, прежде чем
превратиться в действительность и стать материальными моделями, существуют
первоначально в человеческой голове как некоторые теоретические схемы. В этом
смысле их можно назвать идеальными. Эти модели могут быть названы идеальными
также и потому, что все преобразования в них, все переходы в другое состояние,
все преобразования элементов осуществляются мысленно, т. е. в сознании человека.
Особенность идеальных моделей состоит в том, что, согласно Ф. Энгельсу, они не
обязательно воплощаются в действительность.
Идеальные модели могут быть разделены на три группы:
1) образные,
2) знаковые,
3) образно-знаковые.
Образные модели характеризуются тем, что, во-первых, элементы, из которых
конструируются такие модели, представляют собой образы каких-либо реальных,
хорошо известных явлений, доступных непосредственному наблюдению, и, во-вторых,
некоторые свойства и отношения моделируемых явлений представлены в этих моделях
в форме, доступной чувственности. Значит, можно сказать, что образные модели
являются наглядными образами элементов, структуры и поведения объектов. Эти
модели часто фиксируются в виде рисунка, чертежа, схемы.
В знаковых моделях элементы, отношения и свойства моделируемых явлений выражены
при помощи определенных знаков. Особенность таких моделей – это полное и
принципиальное отсутствие сходства между элементами такой знаковой модели и
соответствующими элементами объекта, ибо понятие знака не предполагает подобного
сходства. Таким образом, в отличие от моделей первого рода знаковая модель не
обладает наглядностью в смысле какого бы то ни было сходства ее элементов с
элементами объекта. Но знаковым моделям присущи некоторые элементы наглядности.
Например, структурные формулы в химии.
Образные и знаковые типы моделей образуют два крайних случая. Чаще в идеальных
моделях происходит сочетание первого и второго рода. Эти модели занимают
промежуточное положение. Мы их назвали образно-знаковыми.
Приведенная классификация моделей дает основу для анализа двух основных функций
моделей: практической и теоретической.
Практическая функция моделей состоит в том, что они используются в качестве
орудия или средства научного эксперимента в его специфической форме, связанной с
использованием материальных моделей.
Теоретическая функция моделей реализуется при их использовании в качестве
специфического образа действительности, в котором соединяются элементы
логического и чувственного, абстрактного и конкретного, общего и единичного,
наглядного и не наглядного.
ПОСТРОЕНИЕ МОДЕЛЕЙ В РАЗЛИЧНЫХ ПРЕДМЕТНЫХ ОБЛАСТЯХ
Моделирование в различных предметных областях, как мы уже отмечали, процесс
сложный и трудоемкий. Один из важнейших вопросов при его осуществлении состоит в
выборе наиболее адекватной модели для изучения отдельного объекта, явления,
свойства объекта из определенной предметной области. Можно ставить вопрос о
целесообразном использовании определенных видов моделей для исследования явлений
из той или иной предметной области. При этом нужно иметь в виду, что
математические модели признаются сегодня универсальными практически для всех
предметных областей. С помощью этих моделей могут быть описаны объекты,
принадлежащие практически любой предметной области.
При построении математической модели очень важно хорошо представлять специфику
соответствующей предметной области. Только в этом случае возможно выбрать
подходящие методы и средства моделирования.
Рассмотрим в качестве примеров подходы, которые используются при построении
моделей в таких различных предметных областях, как экономика и естествознание.
При построении математической модели развивающейся экономической системы следует
учитывать ряд особенностей, которые относятся к самой системе (основные ее
компоненты, связи между ними), условиям (воздействиям, которые на нее
оказываются) и результатам ее функционирования (предсказание стабильности работы
системы при изменении некоторых условий, вывод о стабильности системы). Учет
всех этих особенностей при создании модели и описание их с единых математических
позиций (выбор единого математического метода описания) иногда называют
системным подходом.
При создании математической модели экономической системы необходимо выделить все
множество элементов, которое образует эту экономическую систему. Среди этих
элементов есть как производственные, так и непроизводственные процессы.
Необходимо все это множество элементов представить как единую, взаимосвязанную
совокупность.
Кроме того, особенности сферы экономической жизни требуют, чтобы модель включала
не только описание экономических процессов (производства, распределения и т.
д.), но также и описание экономических механизмов регулирования (рыночных,
планового хозяйства и т. п.). При этом из экономической теории следует, что
экономические механизмы регулирования лучше описывать в макропоказателях,
поскольку они отражают усредненные взаимодействия многих людей.
Макрохарактеристики получают обычно путем усреднения исходного микроописания.
При создании модели необходимо учитывать различные воздействия, которые
оказываются на экономическую систему изнутри и извне. Так, все производственные
и непроизводственные процессы осуществляются при непосредственном участии людей,
которые оказывают влияние на их протекание. При этом важны и квалификация, и
уровень образования, и культурные традиции, и многие другие факторы, которые
необходимо учитывать.
На макроэкономические процессы существенно влияние государства. Поэтому
отражающие это влияние параметры должны быть учтены при построении модели.
Экономическая система испытывает и другие внешние воздействия, в частности
воздействия, связанные, например, с сезонными изменениями климатических условий.
Желательно в модели описать чувствительность системы к таким внешним
воздействиям.
Наконец очень важна оценка построенной модели с точки зрения адекватности
отражения ею реальной экономической системы. В связи с этим построенная модель,
результаты, которые могут быть получены с помощью ее исследования, должны
сравниваться с показателями работы реальной системы. Модель должна в целом
отражать основные показатели развивающейся экономической системы.
Такой подход к моделированию экономических систем является довольно общим и
позволяет дать описание практически любого типа экономического развития. Однако
при моделировании реальных экономических систем возникают существенные трудности
как из-за сложности задачи (большой объем данных, большая скорость изменения
экономических параметров, сложность сбора достоверной информации и т. д.), так и
из-за отсутствия адекватного математического аппарата.
Естественнонаучные системы (физические, химические, биологические и т. д.) в
отличие от экономических систем в большей степени исследованы с точки зрения
наличия математического аппарата, который может использоваться для построения
соответствующих математических моделей. Связано это со знанием фундаментальных
закономерностей функционирования этих систем.
При исследовании естественнонаучных систем сначала необходимо попытаться выявить
законы сохранения, присущие исследуемой системе. Например, закон сохранения
массы, закон сохранения энергии, закон сохранения импульса и т. д. Законы
сохранения могут быть глобальными (справедливыми практически везде и всегда) и
локальными (присущими только исследуемой системе). Подчинение естественнонаучной
системы одному из выделенных законов и определяет выбор соответствующего
математического метода.
Следующий шаг состоит в выражении найденных законов сохранения исследуемой
системы в математической форме. Чаще всего это будет система алгебраических или
дифференциальных уравнений. Заметим сразу, что, возможно, не все из вас знакомы
с понятием дифференциального уравнения. В самом общем смысле дифференциальное
уравнение понимается как уравнение, в котором неизвестное стоит под знаком
дифференциала (производной).
Дальше начинается работа с построенной моделью. Это ее экспертная оценка.
Необходимо попытаться решить найденную систему уравнений аналитически. Если это
не удается, то ее решение осуществляется специальными численными методами с
помощью компьютера. Полученные результаты нужно сравнить с экспериментальными
данными. Если совпадение расчетных значений с экспериментальными данными
удовлетворительное, то созданной моделью можно пользоваться.
Чаще всего, построенные модели для естественнонаучных систем используются для
предсказания какого-либо свойства данной системы с последующей его проверкой в
эксперименте.
Алгоритмизация и программирование
Процесс разработки новых программ для ЭВМ включает в себя:
1) постановку задачи
2) создание алгоритма ее решения
3) реализацию алгоритма на ЭВМ в виде программы
4) отладку программы
Рассмотрим поочередно все эти этапы.
1) Постановка задачи состоит в четком формулировании целей работы. Необходимо
четко определить, что является исходными данными, что требуется получить в
качестве результата, каким должен быть интерфейс программы (т.е. каким путем
будет осуществляться диалог с пользователем) и т.д. Постановка задачи является
чрезвычайно важным этапом работы. Многие специалисты считают, что правильная
постановка задачи это уже полшага в направлении ее решения.
2) Алгоритм- описание последовательности операций, которые нужно выполнить для
решения задачи. Слово «алгоритм» происходит от имени арабского математика
Мухаммеда бен Мусы аль-Хорезми, предложившего в IX веке первые алгоритмы решения
арифметических задач.
Графическая интерпретация алгоритма называется блок-схемой. В качестве примера
рассмотрим блок-схему простого и хорошо всем известного алгоритма перехода улицы
через перекресток, оборудованный светофором
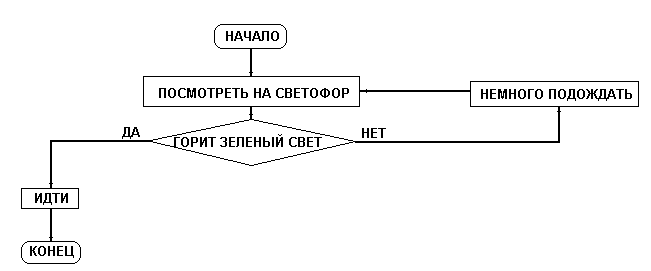
Разработку алгоритма можно сравнить с прокладыванием
трамвайных путей, при котором нужно предусмотреть систему стрелок, разворотов
таким образом, чтобы при любых условиях трамваи могли по проложенным путям дойти
от исходного пункта маршрута к конечному.
Требования к алгоритмам:
отсутствие ошибок.
однозначность, т.е. четкое предписание, что и как делать в каждой конкретной
ситуации. Никаких неоднозначностей («можно сделать так, а можно и так...») быть
не должно. Один из пунктов рассмотренного выше алгоритма перехода улицы звучит
неоднозначно- «немного подождать». Понятно, что данный алгоритм ориентирован на
человека, а человек поймет, что означает слово «немного», правда каждый
по-своему. Для компьютера понятия «немного» не существует, поэтому при создании
машинно-ориентированных алгоритмов нужно указывать конкретные величины, например
«подождать 3 секунды».
универсальность, т.е. применимость данного алгоритма к решению любой задачи
данного типа. Это означает, что если Вы пишите программу для решения квадратного
уравнения, использованный в ней алгоритм должен позволить использовать ее для
решения любого квадратного уравнения, а если Вы пишите программу для создания
мультфильмов, то это нужно делать так, чтобы с ее помощью можно было создавать
любые мультфильмы, и т.д. Данное требование- экономическое. Разработка серьезной
программы это очень сложный, длительный и трудоемкий процесс, и окупится он
только тогда, когда созданная в результате программа будет использоваться
многократно. Писать программы, которые будут использоваться только однажды,
смысла нет. Исключением могут быть только какие-то особые случаи и обучение
программированию.
результативность, т.е. отсутствие зацикливаний. Любая программа должна всегда
приводить к результату, даже если этим результатом будет аварийное сообщение.
Иными словами, рельсы должны быть проложены так, чтобы идущий по ним трамвай в
любой ситуации доехал от начала до конца, т.е. необходимо предусмотреть все
возможные ситуации. Обратимся снова к рассмотренному выше алгоритму перехода
улицы. Очевидно, что если светофор сломан, данный алгоритм не сработает. Иными
словами, эта аварийная ситуация в нем не предусмотрена, и в данном случае,
результат будет не таким, каким должен быть. Конечно, человек, не дождавшись
зеленого сигнала, поймет, что что-то не так и предпримет какие-то действия. Но
компьютер ведь думать не умеет, он как трамвай идет по проложенным рельсам! Если
рельсы проложены так, что аварийная ситуация не предусмотрена, произойдет
зацикливание или будут иметь место какие-либо другие непредсказуемые результаты.
Тогда, в ряде случаев программы «зависают», или зацикливаются, как в
рассматриваемой ситуации. Выйти из образовавшегося замкнутого круга можно только
принудительным прерыванием работы программы, например, путем перезагрузки
компьютера.
3) Следующим шагом после создания алгоритма является написание реализующей его
программы. Основная сложность здесь заключается в том, что программа
представляет собой набор двоичных кодов - нулей и единиц. Алгоритм же
формулируется на естественном человеческом языке- русском, английском, немецком,
арабском и.т.д. Понятно, что перевести текст на естественном человеческом языке
в набор цифр чрезвычайно сложно:
В связи с этим в данный процесс вводится промежуточный этап - разработка текста
программы
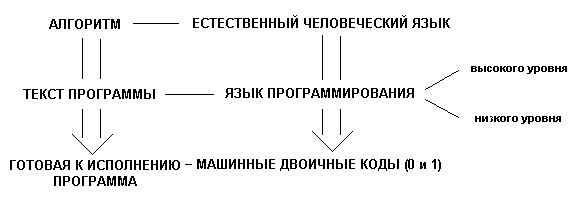
Язык программирования – искусственный язык, являющийся
промежуточным при переходе от естественного человеческого языка к машинным
двоичным кодам. Языки программирования бывают высокого и низкого уровней. Языки
программирования высокого уровня (как видно из схемы) являются более близкими к
естественному человеческому языку по сравнению с языками программирования
низкого уровня. Создание текста программы на языке программирования выполняется
человеком вручную, а перевод текста программы в машинные двоичные коды –
трансляция (англ.translation – перевод) выполняется специальными программами-
трансляторами.
Программирование на языках высокого уровня, очевидно, проще, чем на языках
низкого уровня. Оно не требует глубоких знаний устройства компьютера и поэтому
вполне доступно людям, не являющимися специалистами в вычислительной технике.
Однако, программы, написанные на языках низкого уровня, как правило, отличаются
более высокой скоростью работы, меньшим объемом и более полным использованием
ресурсов вычислительной техники.
К языкам высокого уровня относятся: фортран, БЕЙСИК, ПАСКАЛЬ, СИ, АЛГОЛ, АДА,
СИ++, DELPHI, JAVA и сотни других.
Старейшим языком программирования высокого уровня является ФОРТРАН (англ.
FORmula TRANslation, перевод формул). Он был создан группой программистов
американской фирмы IBM под руководством Джона Бекуса в 1957 году. Несколько
позже в Европе был разработан язык АЛГОЛ (англ.ALGOrythmic Language,
алгоритмический язык). Эти языки послужили основой для других новых языков
программирования. Так, язык БЕЙСИК (англ. basic, базовый, или Beginner's
All-purpose Symbolic Instruction Code, многоцелевой язык символических команд
для начинающих) был создан Джоном Кемени в США в 1965 году. Он представляет
собой упрощенную версию ФОРТРАНА, который оказался сложным для большинства
пользователей из-за своей избыточности. Язык АЛГОЛ послужил основой для не менее
популярного языка ПАСКАЛЯ, созданного в 1969 году швейцарским математиком
Никласом Виртом. ПАСКАЛЬ не сложнее Бейсика, но в него изначально были заложены
более широкие возможности. Дальнейшее развитие язык ПАСКАЛЬ получил в виде
системы программирования DELPHI. На Украине в 1965 году на базе АЛГОЛА был
создан язык АЛМИР, отличавшийся использованием символики на основе русского, а
не английского языка. Этот язык считается первым в мире языком программирования
на основе национального языка (Native Language).
Язык СИ, в котором использованы элементы ПАСКАЛЯ, был создан в 1972 году в
американской фирме Bell Laboratories под руководством Дениса Ритчи. Название
языка СИ связано с тем, что наиболее удачной оказалась его третья версия (СИ-
третья буква английского алфавита). СИ считается наиболее эффективным среди
языков программирования высокого уровня. С одной стороны он не намного сложнее
ПАСКАЛЯ или ФОРТРАНА, но с другой обладает возможностями, присущими языкам
программирования низкого уровня. Поэтому СИ иногда называют языком
программирования среднего уровня и используют как при написании прикладных
программ, так и при разработке системных. Дальнейшим развитием языка СИ стали
языки СИ++ и JAVA.
К языкам низкого уровня отноятся ассемблер и автокод. Ассемблер, как язык
низкого уровня, фактически состоит из набора команд данной машины, записанных в
виде сокращений на английском языке. Автокод- вариант ассемблера на основе
русского языка.
Программы трансляторы бывают двух типов: Интерпретаторы и компиляторы
Интерпретаторы транслируют текст программы и сразу же выполняют предписанные в
нем действия, не создавая .ехе-файл. компиляторы транслируют текст программы и
создают готовую к исполнению программу в виде .ехе-файла, который можно будет
после запустить на исполнение.
4) Отладка программы - исправление в ней ошибок и тщательное ее тестирование.
При тестировании программы важно проверить ее работоспособность как можно в
большем числе ситуаций, например, при различных вариантах исходных данных.
Бывает, что в 1000 случаях программа сработает нормально, а на 1001-й раз
обнаружится ошибка. При написании серьезных программных продуктов для более
полного их тестирования фирмы-разработчики часто распространяют их пробные
версии (бета-версии) среди как можно большего числа пользователей, которые
сообщают в фирму об обнаруженных ошибках, что позволяет исправить их в
окончательных версиях программных продуктов.
|

