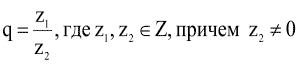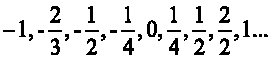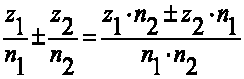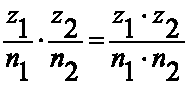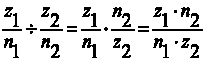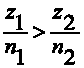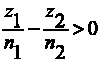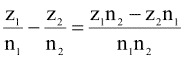Числовые множества

Из школьного курса математики известны натуральные, действительные, рациональные и целые числа.
Натуральные или естественные числа.
Это числа 1, 2, 3, 4, 5 и т. д. Обозначение натуральных чисел: N.
Зачем понадобились натуральные числа? Отвечать на вопросы: «Сколько?» и «Который?».
Сколько студентов в аудитории? Который ряд парт в аудитории содержит больше юношей?
Иногда встречаются ситуации, когда приходится ответить на вопрос: «Сколько человек в аудитории, рост которых больше пяти метров?». Для ответа на этот вопрос математики ввели число ноль, которое обозначается 0.
Множество натуральных чисел состоит из 1, 2, 3, … Их невозможно перечислить, так как для любого натурального числа существует большее. Оно бесконечно.
Допустимые действия с натуральными числами:

1) операции сложения и умножения
a + b = с a · b = с
операции обладают свойствами:
Сочетательный закон
(a + b) + с = a + (b + с) (a · b) · с = a · (b · с)
Например,
(5 + 2) + 3 = 5 + (2 + 3) (4 · 5) · 3 = 4 · (5 · 3)
Переместительный закон
a + b = b + a a · b = b · a
Например,
4 + 6 = 6 + 4 2 · 7 = 7 · 2
2) операции сравнения
Если a > b то a = b + n
Например,
Если 6 > 4, то 6 = 4 + 2

Однако, на множестве натуральных чисел уравнение a + x = b не всегда разрешимо. Например, 6 + x = 4. Также недостаточно натуральных чисел для обозначения температуры воздуха зимой, убытков, обратного движения и т.п.
Поэтому расширяем множество натуральных чисел до множества целых чисел (Рис.1).
Множество целых чисел получается добавлением к натуральным числам противоположных элементов. Эти элементы называются отрицательные числа .

Целые числа – это числа вида n, – n и 0, где n – натуральное число.
Обозначение: Z.
Справедливо равенство: a + (-a) = 0
Например, 4 + (-4) = 0 и -3 + (-(-3)) = 0
Разумеется, над целыми числами можно производить те же операции, что и над натуральными, а так же справедливы сочетательный и переместительный законы.
Сравниваются целые числа следующим образом:
1) целое число z больше нуля тогда и только тогда, когда оно натуральное;
2) целое число z меньше нуля тогда и только тогда, когда оно противоположное к натуральному;
3) любое натуральное число больше противоположного к натуральному.
Или общий случай для сравнения целых чисел:
z1 > z2 тогда и только тогда, когда z1 – z2 > 0

Итак, теперь можно складывать (+), вычитать (-) и умножать (·) целые числа. Вам хорошо известна операция деления (÷). Всегда ли можно решить уравнение с помощью целых чисел. 4 ÷ 7 = ? Очевидно, что результатом будет являться число нецелое.
   Построим множество рациональных чисел Q .
Любое рациональное число можно представить в виде частного двух целых чисел, причем второе должно быть отлично от нуля, то есть: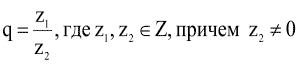

Примеры:

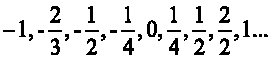
Очевидно, что любое целое число z можно представить в виде дроби .
Каждую дробь можно сделать несократимой дробью, в которой наибольший общий делитель числителя и знаменателя будет равен 1. Например, 6/4=3/2, где НОД(2,3) = 1.

Напомним операции над дробями:
-сложение и вычитание

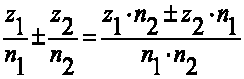
-умножение

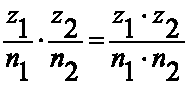
-деление

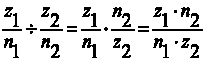
Сравнение дробей:

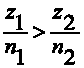
тогда и только тогда, когда 

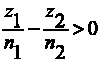
Преобразуем левую часть неравенства:

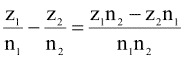
Тогда неравенство выполняется, если z1n2 – z2n1 > 0.
Всегда рациональное число представимо в виде бесконечной десятичной периодической дроби. перация извлечения корня была известна еще в Древней Греции, в Пифагорейской школе. Тогда было открыто существование таких отрезков, длина которых не была равна положительному числу.

Теорема
Не существует такого рационального числа, квадрат которого равен двум.
Доказательство.Пусть – несократимая дробь.
(НОД чисел n и z равен 1)
Тогда  z2 = 2n2  z2 – чётно

Так как квадрат четного числа есть число четное, то z – чётно (а квадрат нечетного числа есть число нечетное: (2n + 1)2 = n2 + 2n + 1)
То есть z нацело делится на 2  z2 нацело делится на 4  n2 нацело делится на 2.
Противоречие: – несократимая дробь.
Что и требовалось доказать.
К рациональным числам (Q) добавим иррациональные числа, которые можно записать бесконечной десятичной дробью, причем непериодической. Таким образом, получим действительные, или вещественные, числа.
Обозначение: R.
Приведем примеры иррациональных чисел: ,,, π и другие.
= 1,4142135623730950488016887242097…
π = 3,141592653…
Можно запомнить последовательность цифр числа Пи следующим образом:
Это(3) я(1) знаю(4) и(1) помню(5) прекрасно(9):
Пи(2) многие(6) знаки(5) мне(3) лишни(5) напрасны(8).

В школе, в старших классах, рисуя числовую прямую для изображения числового интервала, мы изображали именно множество действительных чисел (R). На этой прямой нет такой точки, которой бы не нашлось соответствующего ей числа.
Таким образом, на множестве действительных чисел можно производить и арифметические операции, и операции извлечения корней из положительных действительных чисел. Для извлечения корней из отрицательных чисел математики построили множество комплексных чисел (C).

Полученная нами схема соотношения числовых множеств N, Z, Q, R, C называется «кругами Эйлера-Венна».

Вопросы для самоконтроля:
1. Что можно делать с натуральными числами?
2. Приведите примеры целых, но не натуральных чисел.
3. Какое уравнение не имеет корней на множестве целых чисел?
4. Приведите примеры рациональных, но не натуральных чисел.
5. Приведите примеры рациональных, но не целых чисел.
6. Какие операции можно выполнять с рациональными числами?
7. Что значит десятичная периодическая дробь?