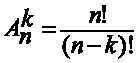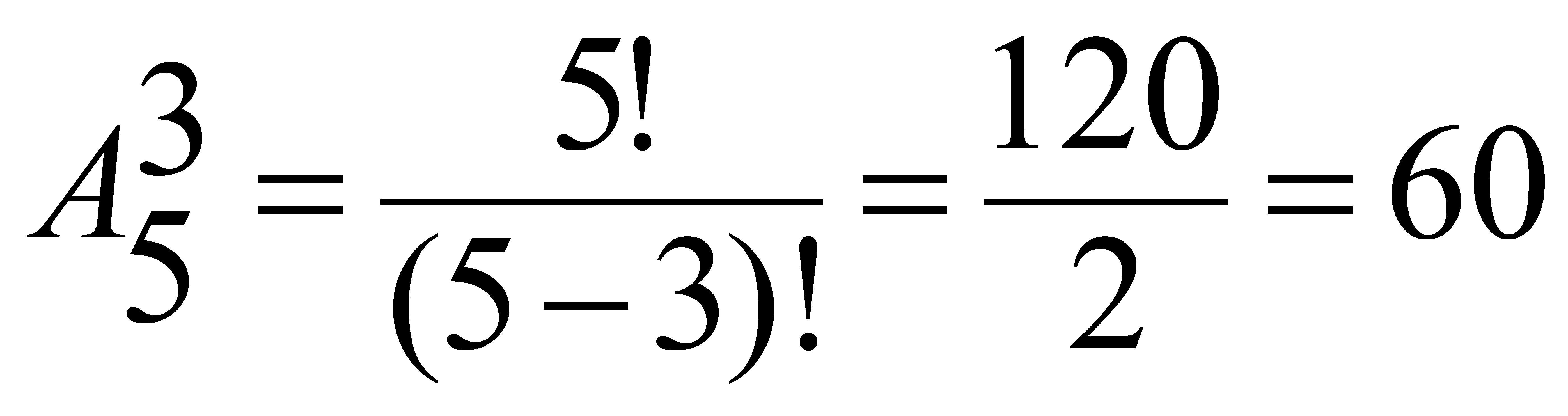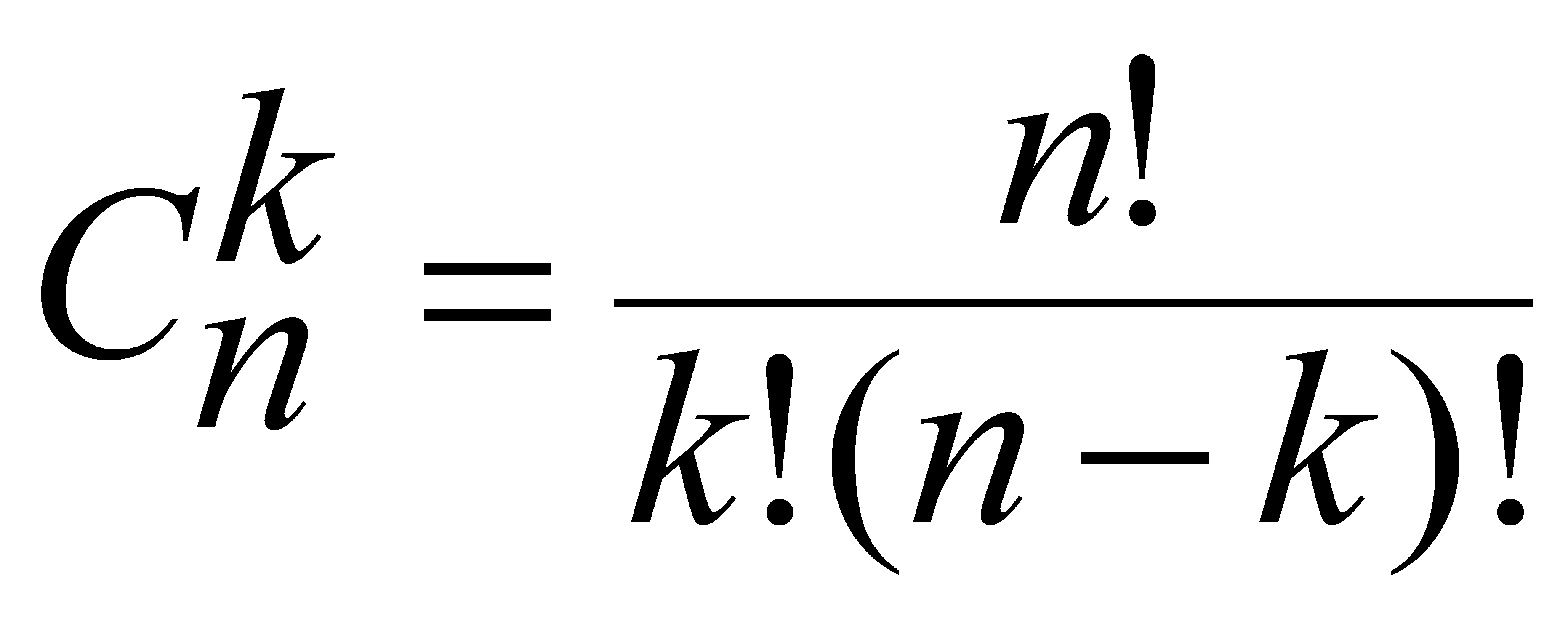Элементы комбинаторики
В математике и ее приложениях часто приходится иметь дело с
различного рода множествами и их подмножествами: устанавливать связь между
элементами каждого из них, определять число множеств или их подмножеств,
обладающих определенными свойствами.
Комбинаторика занимается задачами размещения объектов в соответствии со
специальными правилами и нахождения числа способов, которыми это размещение
может быть сделано. Если способы размещения достаточно простые, то комбинаторика
дает ответ на вопрос о количестве возможных размещений. В более сложных задачах
ставится вопрос о существовании заданного размещения. Мы будем изучать основные
понятия комбинаторики, к которым относятся перестановки, размещения и сочетания.
Правила суммы и произведения. Дерево всевозможных вариантов.
Начнем рассмотрение этого материала с задач:
Задача 1. В магазине есть 5 различных видов коробок конфет и 4 коробки печенья.
Сколькими способами можно составить набор, состоящий из коробки конфет и
печенья?
Для ответа на эти вопросы обратимся к правилу произведения.
Правило произведения: Пусть x принимает одно из n значений X
x {a1, a2, …, an} , y принимает одно из m значений y
x {b1, b2, …, bm}. Тогда для построения упорядоченной пары существует m
x n способов.
Так как всего в таблице m x n клеточек, ответ
очевиден.
|
x
y |
a1 |
a2 |
a3 |
… |
an |
|
b1 |
(a1,b1) |
(a2,b1) |
(a3,b1) |
… |
(an,b1) |
|
b2 |
(a1,b2) |
(a2,b2) |
(a3,b2) |
… |
(an,b2) |
|
b3 |
(a1,b3) |
(a2,b3) |
(a3,b3) |
… |
(an,b3) |
|
… |
… |
… |
… |
… |
… |
|
bm |
(a1,bm) |
(a2,bm) |
(a3,bm) |
… |
(an,bm) |
Решение (задача 1): Одну коробку конфет можно выбрать 5-ю
способами, а печенье – 4-мя. Применяя правило произведения, получим: 45=20.
Правило произведения для двух независимых испытаний удобно показывать, используя
прямоугольники, разбитые на квадратики, или прямоугольные таблицы. Но если
проводятся три испытания, то для иллюстрации надо использовать и длину и ширину,
и высоту, и на картинке получится прямоугольный параллелепипед, разбитый на
кубики. Когда мы имеем дело с четырьмя испытаниями, то для рисунка нам просто не
хватит измерений. (Окружающее нас пространство трехмерно).
Оказывается, правило умножения для трех, четырех и т.д. испытаний можно
объяснить, не выходя за рамки плоскости, с помощью геометрической модели,
которую называют деревом всевозможных вариантов. Она, во-первых, наглядна как
всякая картинка, и, во-вторых, позволяет все учесть, ничего не упустив.
Рассмотрим Задачу 2: Несколько стран в качестве символа своего государства
решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине,
но разных по цвету: белый, синий, красный. Сколько стран могут использовать
такую символику при условии, что у каждой страны свой, отличный от других флаг?
Решение (задача 2):
Будем искать решение с помощью дерева возможных вариантов (Рис 12). Посмотрим на
его левую «веточку», идущую от флага, пусть верхняя полоса – белого цвета, тогда
средняя полоса может быть либо синей, либо красной, а нижняя соответственно,
красной или синей. Получилось два варианта цветов полос флага: белая, синяя,
красная и белая, красная, синяя.
Пусть теперь верхняя полоса – синего цвета, это вторая «веточка». Тогда средняя
полоса может быть белой или красной, а нижняя – соответственно, красной или
белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя,
красная, белая.
Аналогично рассматривается случай для верхней полосы красного цвета. Получится
еще два варианта: красная, белая, синяя и красная, синяя, белая полосы флагов.
Всего 6 комбинаций.
Рассмотрим Задачу 3: На тарелке лежат 5 яблок и 4 апельсина.
Сколькими способами можно выбрать один плод?
Для решения этой задачи, обратимся к правилу суммы.
Правило суммы: Если объект A можно выбрать m способами, а объект B – k
способами, то выбор «либо A, либо B» можно осуществить m + k способами.
Решение (задача 3): по условию задачи яблоко можно выбрать пятью способами,
апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо
апельсин», то его, согласно правилу суммы, можно осуществить 5+4=9 способами.
Размещение, сочетание, перестановка.
Для изучения таких понятий как размещение, сочетание, перестановка нам
понадобится познакомиться с таким числом как факториал. Число факториал было
введено математиками искусственно, для упрощения выражения.
Произведение первых подряд идущих n натуральных чисел договоримся обозначать
через n! (читать: n-факториал), т.е.
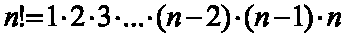
0!=1
1!=1
2!=1∙2=2
3!=1∙2∙3=6
4!=1∙2∙3∙4=24 и т.д.
Рассмотрим произвольное n-элементное множество. Пусть 0<k<n, тогда произвольное
k-элементное подмножество, в котором важен порядок расположения элементов,
называется k-элементным размещением. Количество всех k-элементных размещений на
n-элементном множестве и обозначается.
Теорема:
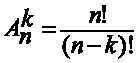
Доказательство
Рассмотрим n-элементное множество A = {a1, a2, a3,…, an}.
1) Берем первый элемент a1, для него существует n способов выбора;
2) для второго элемента a2 существует
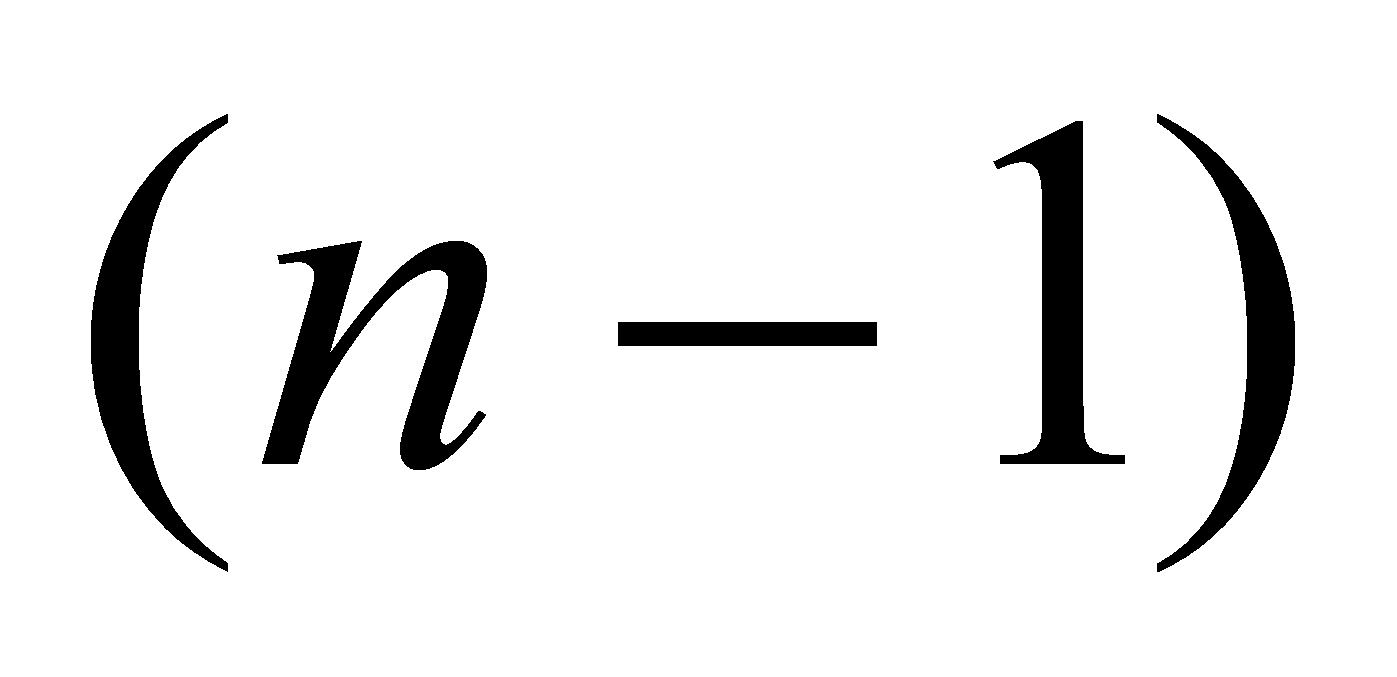 способов
выбора. По правилу произведения пару (a1, a2) можно выбрать способами; способов
выбора. По правилу произведения пару (a1, a2) можно выбрать способами;
3) для третьего элемента a3 существует 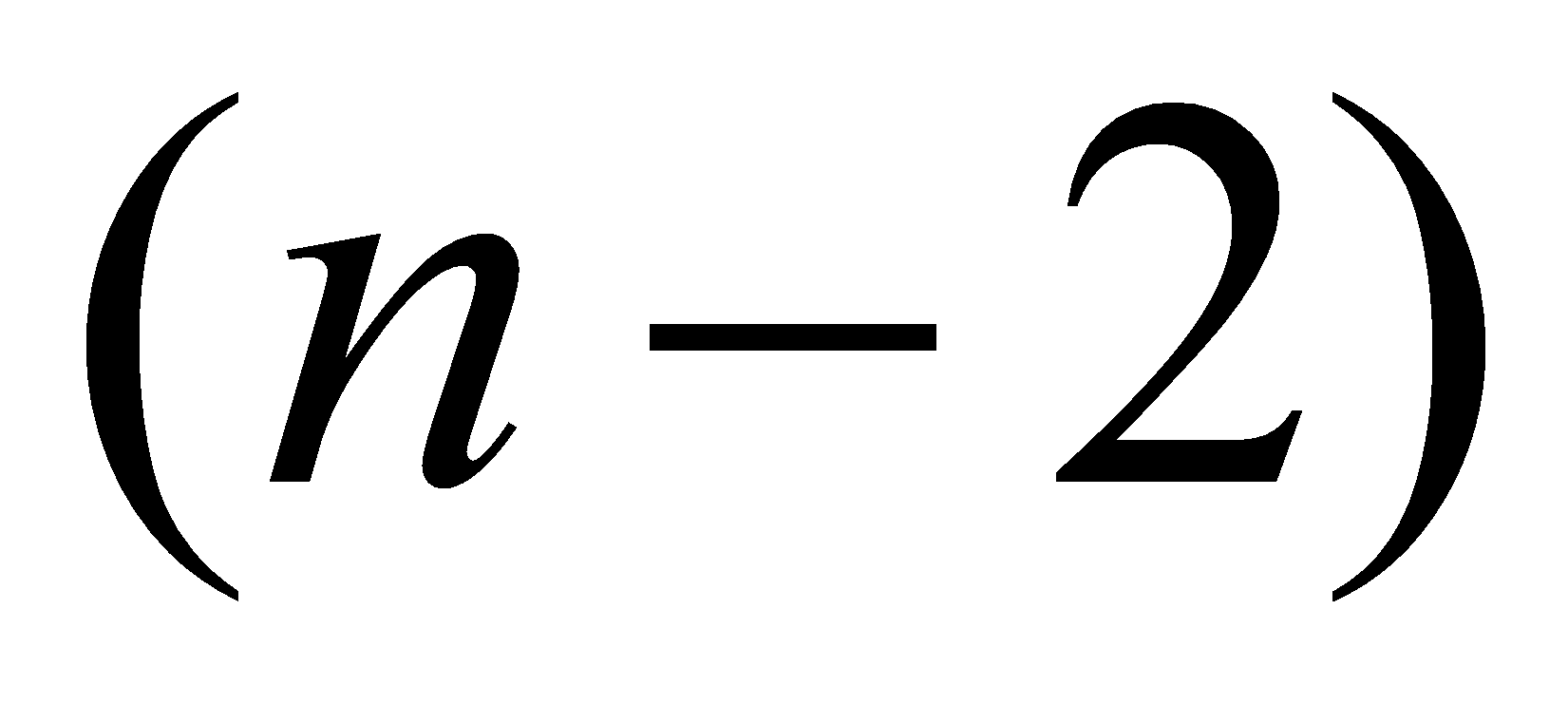 способа
выбора; способа
выбора;
(a1, a2, a3)
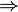
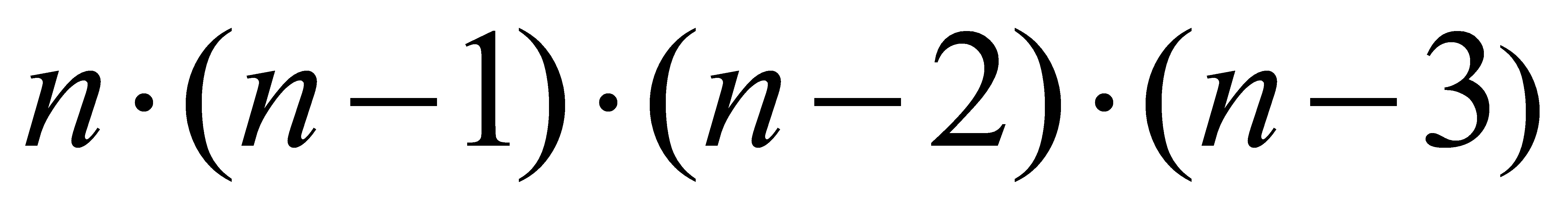 ; ;
4) для k-того элемента ak существует 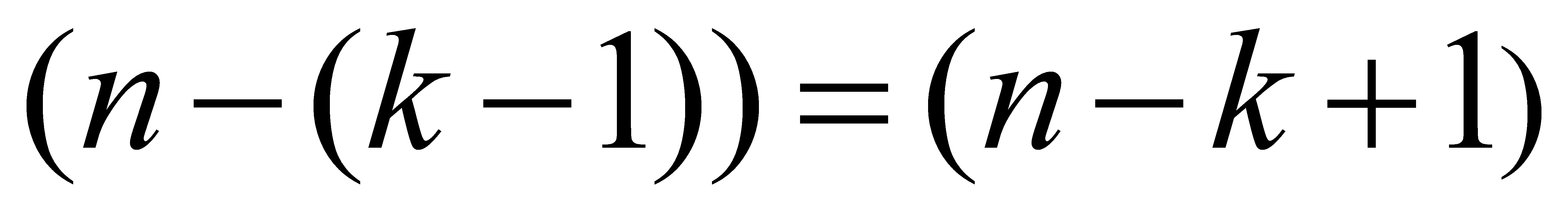 способа
выбора способа
выбора
(a1, a2, a3, …, ak)
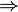 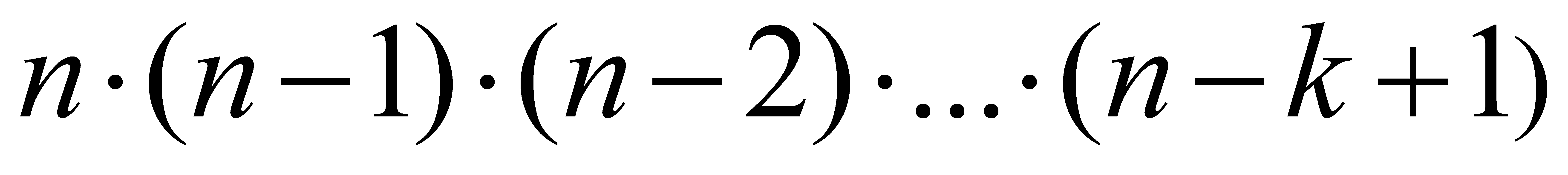 ;
;
5) получим, что упорядоченный набор из k элементов можно выбрать:
умножим и разделим произведение на
 и по
определению факториала получим формулу.Что и требовалось
доказать. и по
определению факториала получим формулу.Что и требовалось
доказать.
Решение задачи:
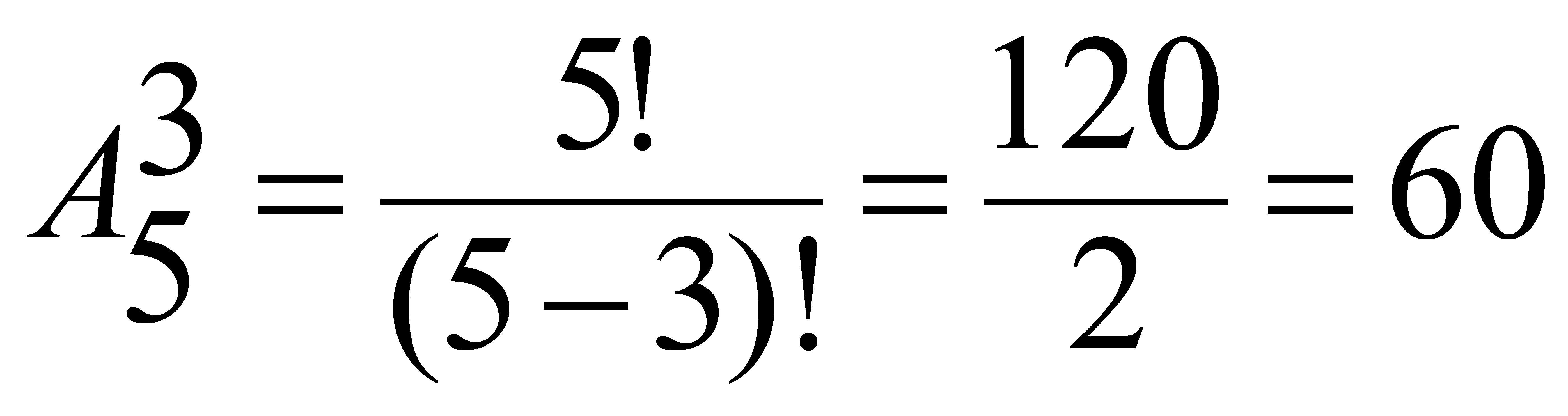
Если k=n, то k-элементное размещение
называется перестановкой для n-элементного множества. Количество всех
перестановок на n-элементном множестве обозначается
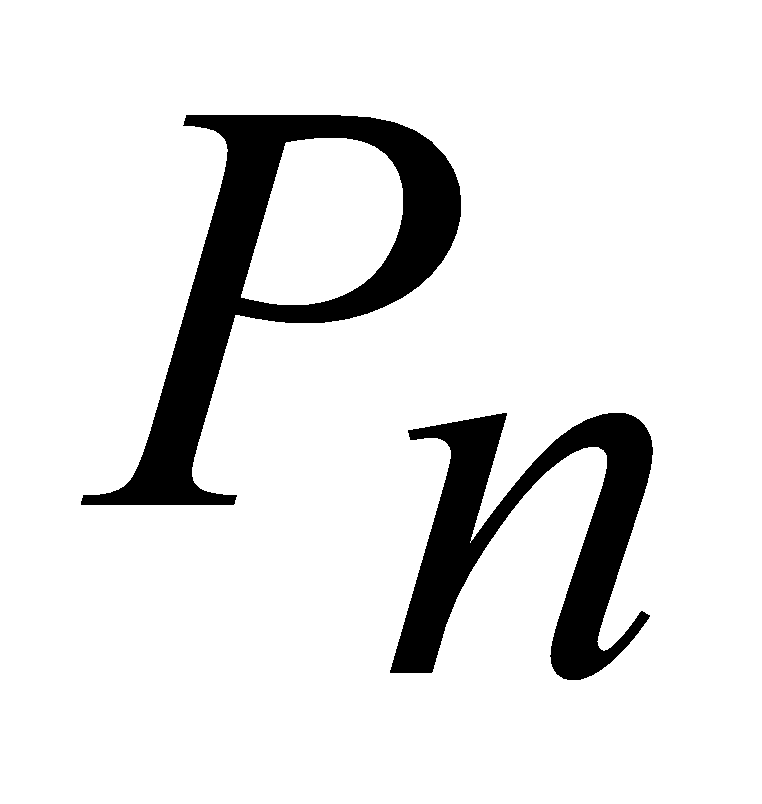 или:
Упорядоченную выборку элементов из некоторого множества будем называть
перестановкой. или:
Упорядоченную выборку элементов из некоторого множества будем называть
перестановкой.
Теорема: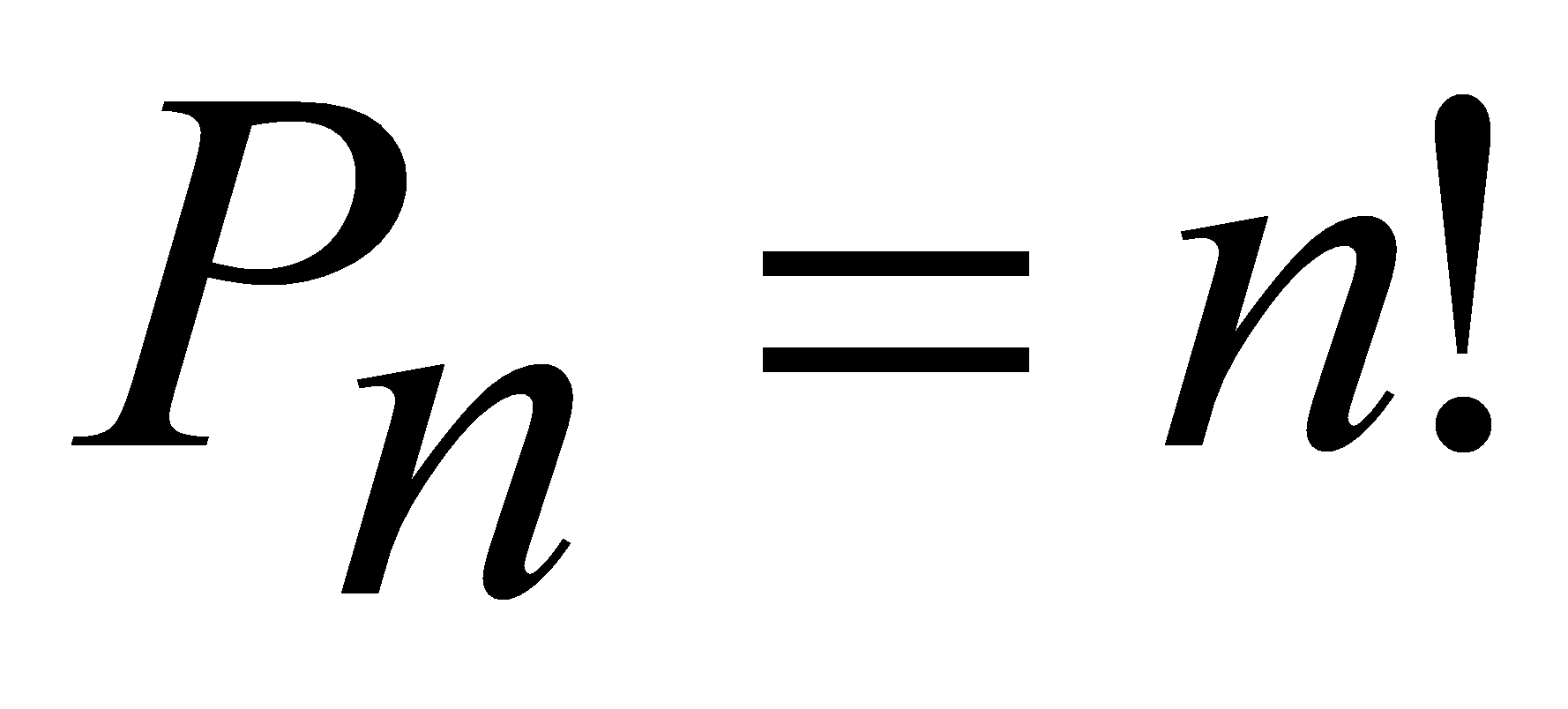 Без
доказательства. Без
доказательства.
Рассмотрим Задачу 4: Имеется пять различных цифр: {1,2,3,4,5}. Сколько различных
5-тизначных чисел с помощью них можно построить.
Решение (задача 4):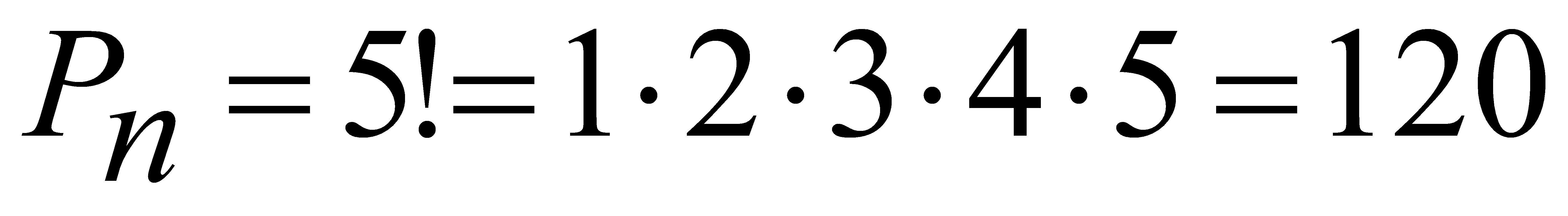
K-элементное подмножество n-элементного
множества называется сочетанием, если порядок расположения элементов не важен.
Количество всех k-элементных сочетаний на n-элементном множестве обозначается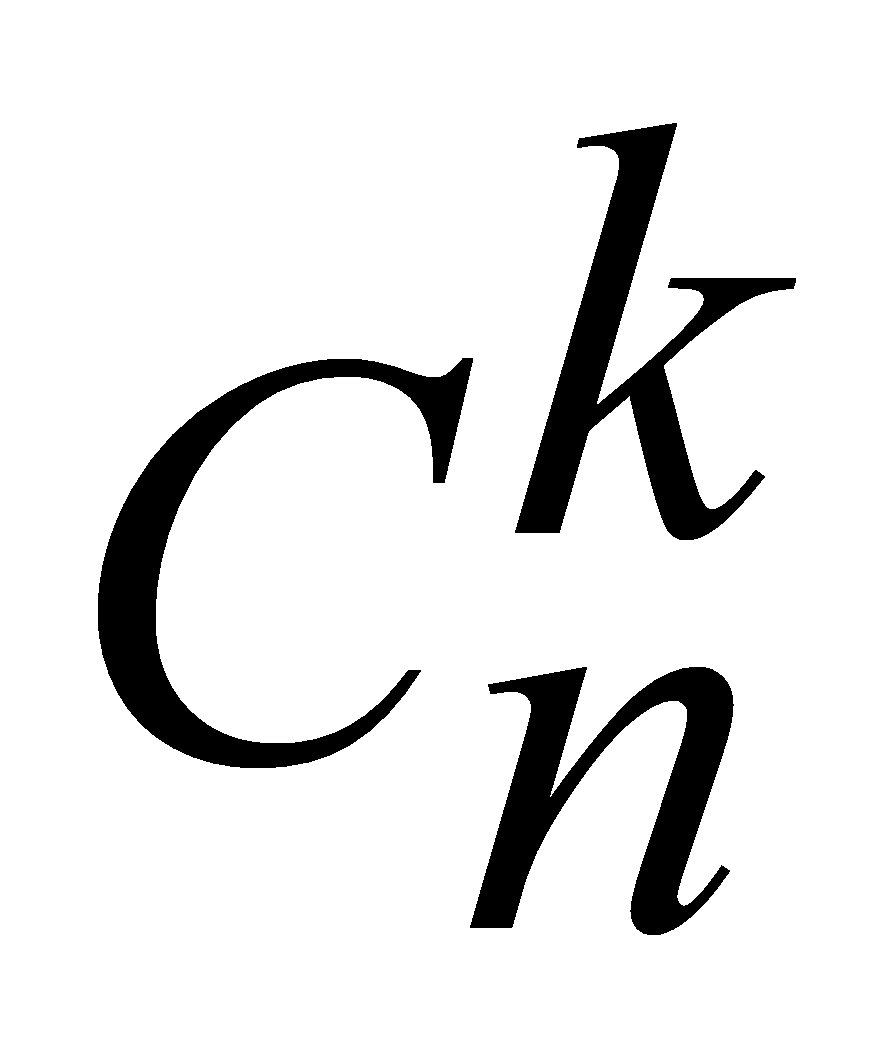 Теорема: Теорема: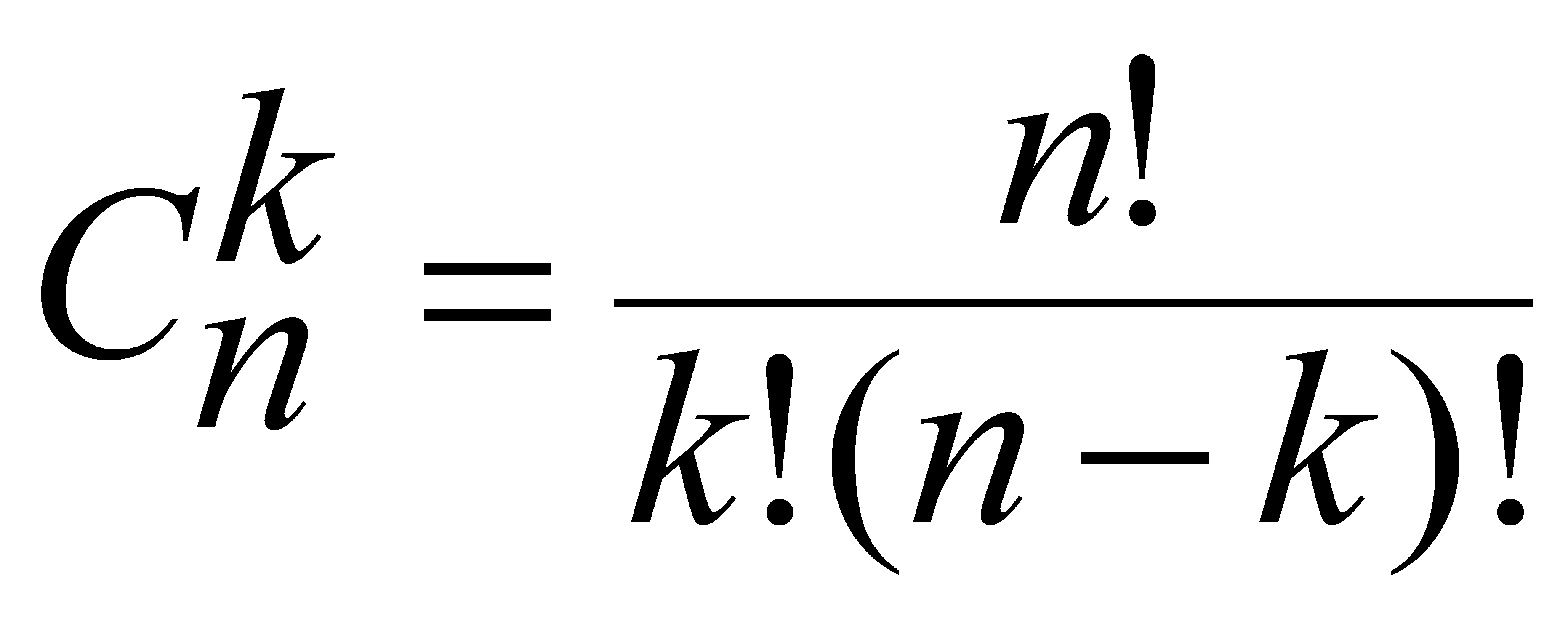
Без доказательства.

|