Энергия электрического поля                          

Электрическое поле способно совершать работу над электрическими зарядами, следовательно, оно обладает энергией (потенциальной).  Вычисления проведём на примере плоского конденсатора (это удобно, так как всё поле сконденсировано между пластинами). Рассуждаем так: с помощью электрического поля перенесём все заряды с одной пластины на другую и посчитаем совершённую при этом работу. Очевидно, эта работа и будет равна запасённой (потенциальной) энергии поля в конденсаторе, ибо когда мы перенесём последний элементарный заряд, энергия израсходуется полностью, то есть само поле исчезнет. (Изменение потенциала отрицательно, работа сил поля положительна.)

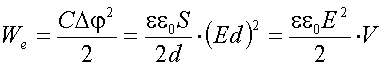
V - объём конденсатора (объём поля)

Формула в рамке верна всегда, для любого электрического поля (в т.ч. переменного).