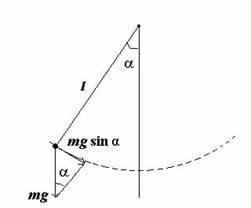
Рассмотрим так называемый математический маятник - материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.

| Второй закон |
|
для такого маятника запишется так: |
![]() ,
или
,
или ![]()
Сравнивая его с дифференциальным уравнением гармонических колебаний (2), увидим, что оно по виду будет совпадать, если sina заменить на a, что можно сделать при малых a. Следовательно, колебания математического маятника можно считать гармоническими только при малых углах отклонения от положения равновесия.
Итак, гармонические колебания математического маятника описываются уравнением
![]()
Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника
![]()
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси O (оси качания), не проходящей через центр инерции тела C.
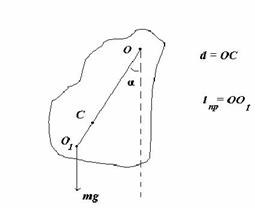
На рисунке обозначено:
ось качания маятника - неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;
точка подвеса маятника О - пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;
приведенная длина физического маятника L пр - длина математического маятника, имеющего такой же период колебаний;
центр качания физического маятника - О1.
Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:
![]()
где J - момент инерции маятника относительно точки О.
Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда sin a @ a. В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:
![]()
Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:
![]()
Из определения приведенной длины физического маятника найдем, что:
![]()
Здесь Jc - момент инерции относительно центра масс тела С.
Центр качания О1 обладает тем свойством, что, если ось качания провести через О1, частота колебаний маятника не изменится, а центр качания будет располагаться в точке О. То есть точки О и О1 обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки О и О1 и сравнить эти формулы.
Рассмотрим пружинный маятник (или в общем случае так называемый линейный гармонический осциллятор), то есть материальную точку массой m, совершающую линейные гармонические колебания под действием упругой силы F:
F = - k x (для пружины это - закон Гука).
Второй закон Ньютона для такого маятника запишется так:
![]() ,
или
,
или
![]()
Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:
![]()