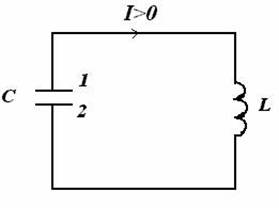
Рассмотрим замкнутую электрическую цепь, состоящую из конденсатора емкостью С и катушки индуктивностью L, без активного сопротивления. Такая цепь называется идеальным колебательным контуром.

Если конденсатор был предварительно заряжен, то после замыкания цепи в ней пойдет ток. Закон Ома для участка цепи 1 - L - 2 запишется следующим образом:
![]()
где Е - э.д.с. самоиндукции.
Если в этом уравнении сделать подстановки:
![]()
![]()
![]()
то придем к следующему уравнению относительно заряда q:
![]()
Сравнивая его с уравнением свободных гармонических колебаний, видим, что полученное уравнение также является уравнением свободных гармонических колебаний заряда на обкладках конденсатора с циклической частотой:
![]()
Колебания заряда в контуре происходят по закону:
![]()
|
сравните с уравнением колебаний маятника,
|
а колебания тока -
![]()
В этих формулах: q0 - амплитуда заряда, I0 - амплитуда тока,
![]()
Ток в контуре опережает заряд конденсатора по фазе на p/2.
Разность потенциалов на обкладках конденсатора также меняется по синусоидальному закону (синхронно с колебаниями заряда):
![]()
Амплитуду тока можно выразить через амплитуду напряжения:
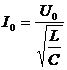
В таком виде формула напоминает закон Ома, а размерность знаменателя соответствует размерности сопротивления. Поэтому величину, стоящую в знаменателе называют волновым сопротивлением контура. Это сопротивление не следует путать с активным сопротивлением R (которого в нашем идеализированном контуре нет). Сопротивление изменяющемуся току оказывают не столкновения носителей заряда (электронов) в проводнике с ионами кристаллической решетки с безвозвратной потерей электромагнитной энергии, а э.д.с. самоиндукции в катушке в соответствии с законом
|