Математика и информатика

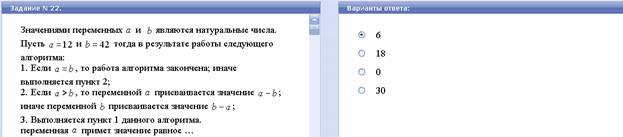
Декартовым произведением множеств X и Y называется множество, обозначаемое X×У, элементами которого являются упорядоченные пары (x;у), где х X, у Y.

Алгебра логики — раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными и ложными.

Логические операции Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:B = { Ложь, Истина }.Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ) $\lnot$ отрицание, конъюнкции (И) $\land$ конъюнкция и дизъюнкции (ИЛИ) $\lor$ дизъюнкция определяются в привычном нам понимании. Существуют и другие логические операции.

1. Операция, выражаемая связками “если ..., то”, “из ... следует”, “... влечет ...”, называется импликацией.

2. Операция, выражаемая связками “тогда и только тогда”, "необходимо и достаточно”, “... равносильно ...”, называется эквиваленцией или двойной импликацией.

Математическое ожидание дискретного распределения Если $X$ — дискретная случайная величина, имеющая распределение 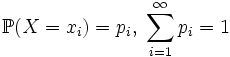$\mathbb{P}(X=x_i) = p_i,\; \sum\limits_{i=1}^{\infty} p_i = 1$ , то прямо из определения интеграла Лебега следует, что $M[X]=\sum\limits_{i=1}^{\infty} x_i\, p_i$ .

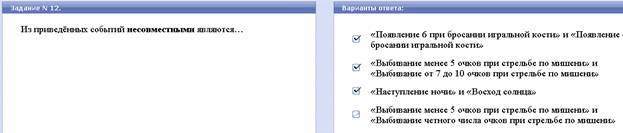
Ø События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания

Ø Случайные события называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Определим основные понятия математической статистики.

Генеральная совокупность – все множество имеющихся объектов.

Выборка – набор объектов, случайно отобранных из генеральной совокупности.

Объем генеральной совокупности N и объем выборки n – число объектов в рассматриваемой совокупности.

Виды выборки:

Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность;

Бесповторная – отобранный объект в генеральную совокупность не возвращается.

Замечание. Для того, чтобы по исследованию выборки можно было сделать выводы о поведении интересующего нас признака генеральной совокупности, нужно, чтобы выборка правиль-но представляла пропорции генеральной совокупности, то есть была репрезентативной (представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем для любого объекта вероятность попасть в выборку одинакова.

Первичная обработка результатов.

Пусть интересующая нас случайная величина Х принимает в выборке значение х₁ п₁ раз, х₂ – п₂ раз, …, х_к – п_к раз, причем где п – объем выборки. Тогда наблюдаемые значения случайной величины х₁, х₂,…, х_к называют вариантами, а п₁, п₂,…, п_к – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – статистическим рядом:

x_i	x₁	x₂	…	x_k
n_i	n₁	n₂	…	n_k
w_i	w₁	w₂	…	w_k

Пример.

При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Статистический ряд для абсолютных и относительных частот имеет вид:

x_i	0	1	2	3	4	5
n_i	3	6	5	3	2	1
w_i	0,15	0,3	0,25	0,15	0,1	0,05

Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:

Решение: (1/7)*21=3

Решение: 8-7=1

http://cito-web.yspu.yar.ru/link1/metod/theory/node39.html

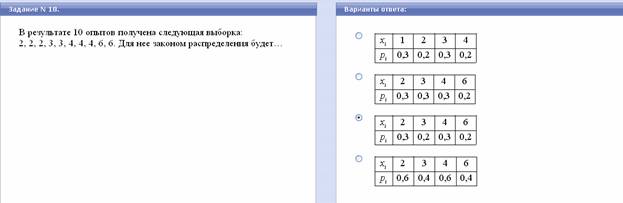
Решение: 3/10=0,3; 2/10=0,2.

Выборочная медиана – это середина вариационного ряда (см.Турецкий В.Я., с.405)

(элементы выборки x₁, x₂,…, x_nрасположить в порядке неубывания)