вне шара | внутри шара | потенциал | графики
| Поле и потенциал
заряженного шара |
вне шара | внутри шара | потенциал | графики |
|
Пользуясь тем, что гауссова поверхность (в законе Гаусса) произвольная, выберем её как нам удобнее, а удобнее взять её в виде шаровой сферы, концентрической с нашим заряженным шаром. При этом, в силу симметрии, на всей гауссовой поверхности электрическое поле будет одинаково. Выносим его из под знака интеграла в законе Гаусса: |
|
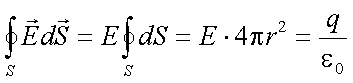
|
То есть |
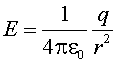
|
- вне шара такое же поле, как от точечного заряда. |
Для нахождения поля вне шара не важно, как распределён заряд внутри шара - по поверхности, или по объёму; лишь бы симметрично.