Будем считать цилиндр
бесконечно длинным. Заряженность
цилиндра в этом случае будет
характеризоваться линейной плотностью
заряда, то есть зарядом на единицу длины
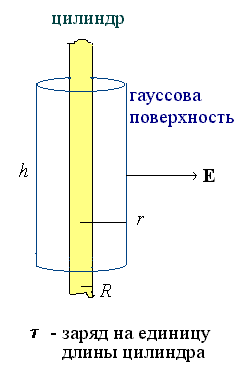
цилиндра. Схема применения теоремы
Гаусса для нахождения поля вне
цилиндра следующая:
- в силу симметрии заключаем, что линии
поля направлены перпендикулярно оси
цилиндра;
- гауссову поверхность строим в виде
цилиндра, соосного с нашим цилиндром;
- заключаем, что через торцевые
поверхности гауссова цилиндра поток
поля равен нулю, так как эти
поверхности параллельны линиям поля;
- на боковой поверхности гауссова
цилиндра величина поля всюду
одинакова - в силу симметрии, поэтому E
в теореме Гаусса можно вынести из-под
знака интеграла;
- в результате теорема Гаусса
принимает вид:
|
|